spyked bricks in the wall

să scriem împreună un generator de text markov (ii)

În cadrul articolului introductiv am prezentat pe scurt ideea de a implementa un generator de text Markov ca exercițiu pur didactic, am explicat câteva din conceptele teoretice fundamentale pe care se constituie aplicația și nu în ultimul rând am definit o structură de date în Haskell, structură care se mapează unu la unu pe cea a unui lanț Markov. Mai departe voi da un exemplu de construcție (non-algoritmică) a unui obiect de tipul Chain, după care vom porni spre a programa un simulator de procese Markov, definit printr-o interfață oarecare, fixă, interfață care la rândul ei se constituie pe baza unor funcții Haskell.

O primă și importantă funcționalitate a acestei interfețe o reprezintă aceea de construire a lanțurilor Markov. Modulul Data.Map oferă tot soiul de modalități de construire a dicționarelor, printre care inserarea, reuniunea etc. Dat fiind că în programarea funcțională cea mai naturală metodă de a reprezenta chestii este lista, noi vom defini o funcție fromList, care se va folosi de omoloaga din Data.Map pentru a construi lanțuri Markov din asocieri stare-listă (de tupluri stare-probabilitate):

fromList :: Ord a => [(a, [(a, Float)])] -> Chain a
fromList = M.fromList

Signatura de tip pare un pic încurcată, o ocazie numai bună pentru a o descurca noi. În primul rând, restricția Ord a impune ca tipul a să aibă definită o relație de ordine totală [i], din rațiuni de implementare a tipului de date dicționar în Haskell. În al doilea rând că lista primită ca argument e o listă de asocieri cheie-valoare, asocieri ale cărei valori sunt la rândul lor liste. Întâmplător, listele în cauză conțin și ele asocieri cheie-valoare (cheia fiind starea și valoarea probabilitatea), ceea ce face din structura noastră de date, într-un anumit sens, un dicționar de dicționare. Nu am folosit însă Map pentru lista de tupluri stare-probabilitate deoarece aceasta e oricum parcursă de la un cap la celălalt, căutarea fiind în acest caz o funcționalitate cvasi-inutilă.

Exercițiu (p2.1): Redefiniți câmpul din tipul Chain asociat valorilor dicționarului, folosind alias-uri de tip — hint: tipul Chain este însuși un alias de tip. Îmbunătățirea este una pur estetică, oferind programatorului o înțelegere mai bună asupra codului.

Având astfel la dispoziție o modalitate de a construi lanțuri Markov prin explicitarea nodurilor și a arcelor, să definim un modul Haskell nou în care să creăm o valoare de tipul Chain Weather, unde Weather e tipul explicitat în cele ce urmează:

module Markov.Examples where
 
import Markov.Chain
 
-- possible states of the weather
data Weather = Sunny | Rainy deriving (Eq, Ord, Show)
 
-- a "Weather Markov chain"
weatherChain :: Chain Weather
weatherChain = fromList [
    (Sunny, [(Sunny, 0.6), (Rainy, 0.4)]),
    (Rainy, [(Sunny, 0.7), (Rainy, 0.3)])
    ]

Observăm că am definit un tip nou de date Weather, cu două valori posibile, Sunny și Rainy. De asemenea am definit lanțul Markov din exemplul dat în articolul anterior, exprimabil prin graful:

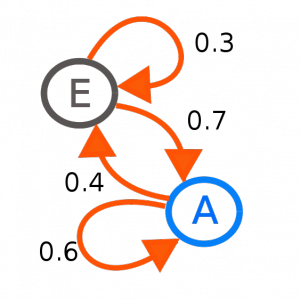
unde 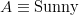și .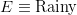

ii.1. implementarea unui simulator de procese markov

Mai departe avem nevoie de o funcție care să întoarcă lista stărilor accesibile dintr-o stare dată, primind un lanț Markov ca valoare. Forma funcției poate fi dată imediat prin folosirea funcției lookup:

accessibleStates :: Ord a => Chain a -> a -> [(a, Float)]
accessibleStates c s = case M.lookup s c of
    Just accs -> accs
    Nothing -> []

Observăm că funcția în sine nu ne este foarte utilă. Pentru programator, scopul final al definirii unui lanț Markov este acela de a-l folosi pentru simularea proceselor cu același nume. Cu alte cuvinte dorim să plecăm dintr-o stare dată (aleasă după criterii date sau aleator) și să executăm așa-zise „plimbări aleatoare” prin graful dat. Utilitatea funcției accessibleStates e aici aceea de furnizor de distribuție de probabilități pentru o stare dată, urmând ca mai departe să folosim distribuția asociată stării curente pentru a alege aleator următoarea stare. Pentru aceasta vom da signatura funcției next:

next :: Ord a => Chain a -> a -> IO a

next primește ca argumente un lanț Markov și o stare a acestuia și întoarce următoarea stare „înfășurată” în monada IO [ii]. Vom folosi funcția pentru a defini o așa-zisă mașină cu stări, care să se plimbe prin graf. Mașina, pe care o vom numi randomWalk, va fi principala metodă de a simula un proces Markov, constituindu-se deci drept un element important al interfeței oferită de modulul Markov.Chain; de asemenea orice plimbare va avea un număr bine determinat de pași, motiv pentru care mai avem nevoie de un argument (pe lângă lanțul Markov și starea inițială) pentru a defini noua funcție; în plus, randomWalk va întoarce nu o stare, ci o listă de stări reprezentând toate stările parcurse de la începutul plimbării și până la încheierea acesteia. Mai jos puteți observa definiția funcției randomWalk:

randomWalk :: Ord a => Chain a -> a -> Int -> IO [a]
randomWalk c s n = if n <= 0
	then return []
	else do
		ns <- next c s
		rw' <- randomWalk c ns (n - 1)
		return $ s : rw'

Forma este tipică programării funcționale: dacă mai am de mers zero (sau mai puțini) pași înseamnă că plimbarea s-a terminat, deci întorc o listă vidă. Altfel iau următoarea stare pornind din starea curentă și merg mai departe. De întors întorc starea curentă plus restul stărilor întoarse de apelul recursiv al lui randomWalk.

Observați însă că am omis să dau definiția lui next, și am făcut-o intenționat deoarece aceasta necesită o discuție un pic mai amplă. next trebuie să facă două lucruri: să genereze un număr aleator între 0 și 1 (asociat unei probabilități) și să îl folosească pentru a alege starea următoare. Prima parte poate fi comisă cu ajutorul funcției randomRIO. A doua parte e un pic mai complicată și necesită două funcții auxiliare, după cum se poate vedea în definiția de mai jos:

next c s = do
    rn <- randomRIO (0, 1)
    return $ next' rn 0 $ sortByProb $ accessibleStates c s

În primul rând next ia stările accesibile din starea curentă și le sortează după probabilitate, folosind funcția sortByProb:

sortByProb :: [(a, Float)] -> [(a, Float)]
sortByProb = sortBy (.<.)
    where
    sp .<. sp' = snd sp' `compare` snd sp

Apoi next' ia lista de stări sortată și face o eșantionare după algoritmul ruletei, care ia cea mai probabilă stare și verifică dacă numărul generat se încadrează în aceasta. Dacă da atunci o selectează, altfel adună probabilitatea asociată stării-țintă eșuată și verifică din nou, folosind următoarea stare ca probabilitate și așa mai departe. Codul pentru next' este dat în următorul paragraf:

    next' _ _ [] = error "No states available."
    next' _ _ (sp : []) = fst sp
    next' rn acc ((s, p) : sps) = -- sample
        if rn <= acc + p
            then s
            else next' rn (acc + p) sps

Parametrul acc e folosit pentru „incrementarea” ruletei, cu observația că nu se fac verificări legate de depășirea valorii 1. Cu alte cuvinte nu se verifică normalizarea distribuției de probabilitate, această povară fiind lăsată pe seama utilizatorului. Altfel și next' e tipică programării funcționale, neexistând aspecte deosebite în legătură cu aceasta.

ii.2. testarea simulatorului de procese markov

Acum că avem la dispoziție implementarea unei mașini pseudo-non-deterministe [iii], rămâne să o testăm folosind exemplul ilustrat la începutul articolului. Putem face asta pe loc, încărcând modulul Markov.Examples în mediul interactiv GHCi. În primă fază să testăm afișarea lanțului weatherChain:

*Markov.Examples> weatherChain 
fromList [(Sunny,[(Sunny,0.6),(Rainy,0.4)]),(Rainy,[(Sunny,0.7),(Rainy,0.3)])]

Lanțul arată exact cum l-am definit, deci să testăm în primă fază apelul randomWalk folosind weatherChain ca lanț și Sunny ca stare de plecare, limitând numărul de pași la 5. Semnificația acestui calcul este echivalentă cu rezolvarea problemei „dacă astăzi e soare, care va fi vremea peste o zi, două, trei sau patru?”.

*Markov.Examples> randomWalk weatherChain Sunny 5
[Sunny,Sunny,Sunny,Rainy,Rainy]

Răspunsul pare a fi „astăzi e soare, deci posibil că peste o zi și peste două zile va fi soare, pe când peste trei zile și peste patru zile posibil că va ploua”. Acel „posibil” denotă însă o realitate posibilă și nu deterministă. În universul nostru simulat am colapsat o închipuită „funcție de probabilitate”, dat fiind faptul că semnificația lanțului Markov e aceea a unei distribuții de probabilitate, deci a unei superpoziții de stări. La fel ca în cazul mecanicii cuantice [iv], universul nostru se află atât în starea „însorit” cât și în starea „ploios” până în momentul în care ajungem să îl observăm, moment în care ajungem fie într-una, fie în cealaltă, după cum ne-o fi norocul.

Pentru a ilustra non-determinismul, să rulăm din nou exemplul de mai devreme:

*Markov.Examples> randomWalk weatherChain Sunny 5
[Sunny,Rainy,Sunny,Sunny,Sunny]

Iată că de data asta răspunsul a fost complet diferit: la o zi distanță plouă, iar la două, trei și respectiv patru zile distanță e însorit. O observație în acest sens ar fi aceea că probabilitatea stării următoare e strict condiționată de valoarea stării curente, ajungându-se efectiv la un lanț (în sensul algebric al cuvântului) de dependențe condiționale. Generatorul meu de evenimente aleatoare trebuie însă cu orice preț să respecte distribuțiile date, adică în medie să genereze Sunny cu o probabilitate de 60% și Rainy cu 40% dacă în momentul curent de timp sunt în Sunny, și respectiv 70% și 30% dacă sunt în Rainy.

Putem să testăm imediat acest lucru: iterăm procesul de mai sus cu doi pași în loc de cinci și alegem mereu pasul al doilea (adică elementul cu indexul 1 din lista-rezultat). De exemplu:

*Markov.Examples> sequence $ take 10 $ repeat $ randomWalk weatherChain Sunny 2 >>= return . (!! 1)
[Sunny,Sunny,Rainy,Sunny,Sunny,Sunny,Sunny,Rainy,Sunny,Sunny]

apelează randomWalk cu argumentele de mai sus și trimite rezultatul către o funcție care întoarce elementul cu indexul 1 din listă. Procesul e repetat de zece ori, și în plus e apelată funcția sequence, care transformă o listă de IO într-un IO de tip listă.

Să generăm zece mii (în loc de zece) de astfel de elemente și să numărăm câte zile „Sunny” și câte „Rainy” avem:

*Markov.Examples> let run = sequence $ take 10000 $ repeat $ randomWalk weatherChain Sunny 2 >>= return . (!! 1)
*Markov.Examples> run >>= return . length . filter (== Sunny)
5958
*Markov.Examples> run >>= return . length . filter (== Rainy)
4037

Observăm deci că din Sunny se ajunge în aproximativ 60% din cazuri în Sunny și în cam 40% din cazuri în Rainy, deci generatorul funcționează cum trebuie. Analog pentru cazul în care Rainy este stare de plecare:

*Markov.Examples> let run = sequence $ take 10000 $ repeat $ randomWalk weatherChain Rainy 2 >>= return . (!! 1)
*Markov.Examples> run >>= return . length . filter (== Sunny)
7099
*Markov.Examples> run >>= return . length . filter (== Rainy)
3035

ii.3. concluzii. exerciții

Nu e deloc surprinzător faptul că estimatorii folosiți în practică pentru diverse aplicații (printre care și prognoza meteo) sunt construiți similar. Trebuie menționat totuși că sistemul prezentat aici e peste măsură de primitiv (și deci din capul locului imprecis), fiind proiectat în scopuri didactice. Construirea modelelor statistice e o disciplină în sine, foarte utilă de altfel în ingineria de orice fel [v].

Dat fiind faptul că atât limbajul de programare folosit cât și în sine subiectul tratat pot părea de-a dreptul neprietenoase, propun cititorului rezolvarea a două seturi de exerciții/probleme, dintre care prima a fost deja prezentată mai sus. Celelalte sunt după cum urmează:

Exerciții de programare:

• (p2.2): Redefiniți tipul Chain folosind cuvântul cheie Haskell newtype, care e în mod clar mult mai potrivit pentru definirea tipului de date care stă la baza problemei, oferind (printre altele) încapsulare. Modificați restul codului conform cu noua definiție. Menționați avantaje și dezavantaje ale folosirii newtype față de alias-uri de tip.
• (p2.3): Redefiniți funcția accessibleStates folosind funcția maybe.
• (p2.4): Redefiniți funcțiile next' și randomWalk folosind gărzi în locul construcțiilor de tipul if-then-else.
• (p2.5): Reimplementați next folosind o altă schemă de „sampling”. Explicați felul în care e afectată distribuția stărilor accesibile, dacă e cazul.

Exerciții de teorie:

• (t2.1): Adăugați-i o nouă stare, „Foggy”, exemplului weatherChain. Definiți noile probabilități „după ureche”, având însă grijă ca acestea să fie normalizate.
• (t2.2): Adăugați-i o nouă variabilă, „Wind”, lanțului Markov care prezice vremea. Gândiți-vă la corelații între vânt și soare/vreme și alegeți probabilități în concordanță cu asta. Stările posibile ale noii variabile pot fi „Calm”, „Windy”, „VeryWindy” și orice altă stare care pare ok.
• (t2.3): Experimentați cu exemplele de mai sus și trageți niște concluzii preliminare.

Următorul articol va continua cu exemple pe temă, exemple care vor ghida cititorul către una din întrebările centrale care alcătuiesc problema noastră, aceasta fiind: cum putem construi un model (lanț Markov) care să ajute la generarea aleatoare de text?

1. Sau mai bine zis o așa-zisă „ordonare naturală”. Pentru mai multe detalii consultați documentația asociată clasei de tipuri Ord. [↩]
2. Tipul IO e un tip ceva mai dubios din Haskell, care îi permite utilizatorului să facă tot soiul de chestii practice precum citirea de la tastatură, scrierea într-un fișier sau desenarea unei interfețe grafice. Întâmplător generarea unui număr aleator presupune folosirea facilităților oferite de sistemul de operare, iar starea următoare fiind aleatoare nu poate fi furnizată către utilizator decât sub această formă.

   Aici discuția se poate întinde asupra motivului pentru care am ales să proiectez astfel această funcție și alte considerente, discuție pe care o putem muta într-un articol separat la cerere. Pe moment, cei interesați de monade în general și de IO în particular pot consulta Wiki-ul Haskell. [↩]

3. În virtutea faptului că algoritmii care stau la baza generării „random walk”-ului sunt pseudo-aleatori. [↩]
4. Cu ocazia asta încercăm să înțelegem și intuiția din spatele acestei ramuri cel puțin ezoterice — în sensul că-i greu de înțeles, să nu vă imaginați tot felul de prostii — a fizicii. [↩]
5. Dacă doriți să aprofundați domeniul, vă recomand cu căldură cartea Pattern Recognition and Machine Learning a lui Christopher Bishop, o carte greoaie până și pentru cei familiarizați cu matematicile însă care prezintă bazele unui domeniu din ce în ce mai popular atât în cercetare cât și în industrie. [↩]