spyked bricks in the wall — să scriem împreună un simulator de automate celulare (i)

să scriem împreună un simulator de automate celulare (i)

duminică, 14 oct. 2012, 12:06

Automatele celulare au reprezentat o noutate prin anii ’40-’60, la momentul descoperirii lor de către Ulan și von Neumann. În anii ’70-’80 conceptul a devenit iarăși un subiect de interes datorită cercetărilor (mai degrabă empirice) făcute de Stephen Wolfram și alții pentru a reprezenta și studia diverse trăznăi precum modele ale fizicii digitale sau ale vieții. În anii 1990-2010 descoperirile în cadrul domeniului merg într-un ritm lent, însă nu încetează a se ivi. Cu toate acestea automatele celulare rămân o unealtă educațională extrem de utilă, dată fiind puterea de reprezentare care stă la baza lor. Am arătat deja cum putem modela cu ajutorul acestora un fenomen comun prezent în natură și în mediile sociale, ne mai rămâne doar să punem în practică conceptele prezentate.

Pentru a putea atinge scopul articolului, acela de a construi un simulator de automate celulare, avem nevoie de unelte ajutătoare. Acestea pot fi după caz plăci de textolit, tranzistoare, lămpi, ansambluri hidraulice sau piese LEGO; va trebui însă să mă credeți pe cuvânt că cea mai simplă cale de a implementa un automat celular este scrierea unui program, orice astfel de mașinărie teoretică fiind echivalentă cu cel puțin un subset al unui automat Turing. Din motive în principal egoiste, dar și pentru că doresc să împing mintea cititorului într-un anumit șablon de gândire, aleg să scriu programul care simulează automate celulare în Haskell; nu în C, Python, Java, Ruby sau ce alte fetișuri mai au programatorii în ziua de astăzi, ci într-un limbaj funcțional, care poate transpune în mod natural concepte matematice elementare precum funcțiile în construcții care mai apoi vor rula pe calculator.

Există deci câteva motive pentru care merită să parcurgeți articolul de față și pe cele ce-i vor urma:

Puteți intra în contact direct și neprotejat cu o serie de concepte din programare despre care nu ați auzit până acum, sau ați auzit dar v-a fost frică/lene să le înțelegeți/aprofundați. Cum programarea pe calculator e o disciplină care stă la baza educației oricărui individ, la fel cum stau matematica, fizica, biologia și chimia [i], nu strică niciodată să dați un „refresh” memoriei sau să învățați ce e aia programare declarativă etc.
Vi se dă ocazia să consultați cunoștințe puse pe foaie de oameni care au inventat efectiv calculatoare, dacă nu doar le-au perfecționat. Acestea includ idei din domeniile automaticii și științei calculatoarelor, în jurul cărora au fost concepute unele din cele mai faine chestii din ultima sută de ani. Am trăit șocul absurdității conform căreia automobilele și avioanele sunt bune în timp ce teoria sistemelor nu folosește la nimic, scrierea de față fiind deci în același timp un efort de a vă convinge că teoriile acelea inutile sunt de fapt utile și că în general fenomenele nu apar „pentru că așa le-a dat Dumnezeu”.
Programele sau bucățile de programe pe care le vom implementa aici sunt doar un punct de plecare pentru ce-vreți-voi. Pe Wolfram automatele celulare l-au ajutat să scrie Mathematica; pe cititor îl pot ajuta să își organizeze colecția de filme de dragoste sau să învețe japoneză. Unele persoane nu vor extrage nici un folos practic din demersul ăsta; ce-i drept, nici eu nu i-am găsit vreun folos practic blogului, însă asta nu mă oprește din a-l folosi la tot ceea ce nu-mi folosește.

Menționez că acesta nu este singurul, așa cum nu este nici ultimul ghid de pe Internet care abordează subiectul implementării automatelor celulare. Puteți găsi probabil tutoriale mult mai bine explicate, unele din ele scrise în Haskell. În ceea ce privește limbajul mă aștept să fiți deja oarecum familiari cu idei din măcar primele patru sau cinci capitole din „Learn You a Haskell” și să dați o privire și prin cele mai „avansate”. Nu există „cunoștințe avansate” de Haskell decât dacă ați scris deja un compilator pentru limbaj, caz în care aveți foarte multe să mă învățați. Altfel multe din particularități pot fi prinse „on the fly”, mai ales dacă ați programat în alte limbaje funcționale până acum.

Vom începe exercițiul de programare printr-o declarație de modul, pe care îl vom numi Cell1D:

module Cell1D where
 
import Data.Word (Word8)
import Data.Bits
import System.Random

Am importat modulele Data.Word și Data.Bits pentru că vom reprezenta automatele celulare elementare ca numere pe opt biți. System.Random ne va fi util mai târziu, când vom dori să generăm aleator starea inițială a unui șir de celule.

Implementarea deviază ușor de la modelul prezentat anterior, aceasta bazându-se pe două tipuri de date fundamentale:

type Elementary = Word8
data Cell = E | F deriving Eq

Tipul Elementary reprezintă numeric un automat celular elementar, fiind deci un alias pentru Word8, care se referă la cuvinte (ale mașinii) pe opt biți. Variabilele de tip Cell pot avea două valori posibile, E(mpty) și F(ull) [ii]. Se observă că am derivat automat pentru acesta clasa de tipuri Eq. În plus vrem să putem apela funcția show cu argumente de tip Cell (deci să derivăm manual Show), astfel că vom defini următoarea instanță de tip:

-- Pretty print cells
instance Show Cell where
    show E = "."
    show F = "x"

Astfel o celulă „goală” va fi afișată folosind simbolul „.”, pe când una „plină” va fi notată cu „x”. Momentan această reprezentare textuală e de ajuns, orice alte briz-brizuri grafice putând fi implementate mai târziu.

Automatul propriu-zis poate părea a fi, dacă privim în ansamblu, un fel de chestie care toacă celule într-o veselie și le tot schimbă starea din gol în plin și invers. Această imagine nu e departe de realitate, însă părțile componente ale automatului sunt în fapt foarte simple. Trebuie deci definite câteva funcții auxiliare care să opereze cu celule. O primă astfel de funcție transformă un Cell într-un număr întreg:

-- A cell is equivalent to a bit
cellToNum :: Cell -> Int
cellToNum E = 0
cellToNum F = 1

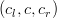
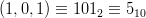
Când am discutat despre reprezentarea pe opt biți a automatelor celulare, spuneam că valoarea unei celule la momentul următor de timp e o funcție de un triplet , astfel că de exemplu , care e un index pentru un vector de biți. Putem folosi deci cellToNum pentru a transforma din baza 2 în baza 10 astfel:

-- A triplet of cells is an index in a list of productions
cellsToIndex :: (Cell, Cell, Cell) -> Int
cellsToIndex (c2, c1, c0) = n2 * 4 + n1 * 2 + n0
    where
    n0 = cellToNum c0
    n1 = cellToNum c1
    n2 = cellToNum c2

Avem însă nevoie și de transformarea inversă. Dorim ca dintr-un vector de biți să obținem un vector (sau o listă) de Cell-uri, care mai apoi va fi indexat(ă) cu ajutorul cellsToIndex. Vom denumi funcția elemToCells:

-- A numerical representation of an elementary cellular automaton
-- corresponds to an indexed list of cells
elemToCells :: Elementary -> [Cell]
elemToCells 0 = []
elemToCells n = c : elemToCells (n `shiftR` 1)
    where
    c = case n .&. 0x1 of
        0 -> E
        1 -> F
        _ -> error "Only binary logic is supported at the moment"

Funcția e foarte simplă dacă ați programat până acum în C folosind operații pe biți. .&. e „și” pe biți; la fiecare pas obținem valoarea celui mai puțin semnificativ bit și o convertim într-un Cell [iii] pe nume c. Apoi deplasăm la dreapta vectorul de biți (cu shiftR) și repetăm operațiile recursiv până când numărul dat ca argument funcției devine zero.

Observăm că lista obținută nu va avea neapărat opt elemente. De exemplu 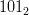e un număr valid care devine zero după trei pași ai algoritmului de mai sus. Din acest motiv va trebui mai încolo să verificăm rezultatul întors de funcție și să „completăm” cu zero (adică E) atunci când este necesar.

Acum putem în final să definim funcția nextCell, care întoarce valoarea celulei după un pas, în funcție de „numărul” automatului și de un triplet de celule oarecare:

-- Transition function for cell triplets
nextCell :: Elementary -> (Cell, Cell, Cell) -> Cell
nextCell n triplet = if length cells >= i then E else cells !! i
    where
    cells = elemToCells n
    i = cellsToIndex triplet

(!!) este funcția de indexare în liste. După cum am explicat anterior, verificăm lungimea listei întoarse de elemToCells înainte de a indexa; în cazul în care indexul se încadrează în listă, se întoarce elementul de pe poziția i. Altfel se întoarce E.

Momentan putem testa apelând nextCell; de exemplu nextCell 184 (E, F, F) ar trebui să întoarcă F, adică „x” [iv]. Data următoare vom completa implementarea simulatorului și vom defini alte câteva funcții auxiliare. De asemenea vom rula două-trei exemple, studiind comportamentul lor în diverse situații.

Această afirmație probabil că nu era adevărată acum douăzeci de ani, însă este de netăgăduit în ziua de astăzi. Copiii trebuie să învețe să opereze cu construcții din programare la fel cum învață să opereze cu gramatica limbii native. [↩]
Aici implementarea diverge de la modelul inițial. În model starea celulelor era dată de o funcție, pe când aici valoarea/starea face parte dintr-o algebră. Observația e relevantă doar în contextul în care am dori să verificăm formal corectitudinea programului, moment în care fie ar trebui să rescriem programul după modelul vechi, fie să construim un alt model. Din fericire în Haskell programele însele sunt un fel de modele atunci când programatorul acordă o foarte mare atenție corectitudinii, mai ales la nivelul tipurilor de date. [↩]
Se face „și” cu 0x1 (în hexa) în loc de 1 (în zecimal) pentru simplul motiv că reprezentarea binară și cea hexazecimală sunt foarte ușor de convertit una în cealaltă. Aici ne puteam lipsi de acest detaliu, însă e foarte bine de ținut minte. [↩]
Consultați explicațiile din „dinamica traficului” dacă nu sunteți lămuriți. [↩]