să scriem împreună un generator de text markov (i)
sâmbătă, 15 dec. 2012, 15:29
Invit cititorul de Cărămizi să ia parte la o inițiativă
- (a) destul de rar întâlnită pe blog-urile românești,
- (b) pur didactică,
- (c) destinată programatorilor amatori, profesioniști sau pur și simplu oamenilor cărora le place să-și folosească chestia aia dintre umeri, și nu în ultimul rând
- (d) aparent inutilă.
De fapt punctul (d) e în mare parte fals; stând un pic și cugetând, realizez că ar fi foarte util să urmăriți tutorialul dacă doriți de exemplu să învățați Haskell sau să vă faceți o idee legată de analiză statistică și lanțuri Markov, sau pur și simplu dacă vreți să vă dezvoltați un generator de spam [i].
Acestea fiind spuse, să începem prin a explica câteva concepte teoretice care stau la baza aplicației noastre. Primul și cel mai important e acela de probabilitate, pe care nu îl voi explica deoarece consider că cititorii mei sunt mai deștepți decât o oaie. Al doilea este acela de probabilitate condiționată, care pleacă de la următorul raționament simplu:
Fie 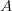 și
și 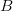 două evenimente. Notăm cu
două evenimente. Notăm cu 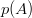 probabilitatea ca
probabilitatea ca 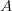 să se fi produs. De asemenea presupunem că am observat producerea lui
să se fi produs. De asemenea presupunem că am observat producerea lui 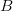 . Acest fapt ne poate oferi informații despre
. Acest fapt ne poate oferi informații despre 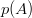 , dat fiind de asemenea faptul că nu știm dacă
, dat fiind de asemenea faptul că nu știm dacă 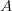 și
și 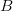 sunt legate cauzal sau corelate sau mai știu eu ce. În cazul ăsta notăm probabilitatea ca
sunt legate cauzal sau corelate sau mai știu eu ce. În cazul ăsta notăm probabilitatea ca 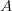 să se fi produs condiționată de
să se fi produs condiționată de 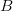 drept
drept 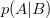 , definită drept raportul dintre probabilitatea conjuncției celor două evenimente și
, definită drept raportul dintre probabilitatea conjuncției celor două evenimente și 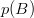 .
.
Privind invers problema, probabilitatea ca atât 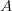 cât și
cât și 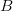 să se fi produs depinde de:
să se fi produs depinde de:
- Probabilitatea ca
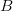 să se fi produs
să se fi produs 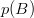 și
și - Probabilitatea ca
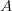 să se fi produs în cazul în care s-a observat
să se fi produs în cazul în care s-a observat 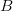 , deci
, deci 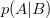 .
.
Din a doua definiție observăm că putem inversa 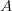 cu
cu 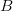 în definiția conjuncției de probabilități, ceea ce ne duce cu gândul că e cam greu de găsit relații de cauzalitate în gândirea probabilistică, dar în fine, astea-s chestii filosofice care nu ne interesează pe noi.
în definiția conjuncției de probabilități, ceea ce ne duce cu gândul că e cam greu de găsit relații de cauzalitate în gândirea probabilistică, dar în fine, astea-s chestii filosofice care nu ne interesează pe noi.
Dacă tot am ajuns aici, să dăm și un exemplu: să presupunem evenimentele mutual exclusive 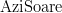 și
și 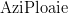 , având semnificațiile evidente „azi e soare” și „azi plouă”. Analog putem defini
, având semnificațiile evidente „azi e soare” și „azi plouă”. Analog putem defini 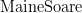 și
și 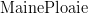 cu semnificații similare. E clară deci relația dintre perechile de evenimente, însă nu sunt clare relațiile inter-perechi, de exemplu dependența dintre
cu semnificații similare. E clară deci relația dintre perechile de evenimente, însă nu sunt clare relațiile inter-perechi, de exemplu dependența dintre 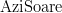 și
și 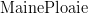 .
.
Dat fiind că ziua de mâine o succede pe cea de azi, putem observa la un moment dat starea de azi a vremii, informație pe care apoi o vom putea folosi pentru a face predicții asupra vremii de mâine. Generalizând, putem folosi probabilitățile condiționate [ii] pentru a face predicții legate de starea vremii în viitor bazate pe starea curentă a vremii. Orice proces asemănător cu cel de mai sus se numește lanț Markov și poate fi reprezentat printr-un graf, după cum se poate vedea în link-ul de pe Wikipedia. Graful va avea pe arce probabilități condiționate, un arc 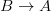 având asociată o valoare
având asociată o valoare 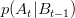
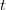 e timpul reprezentat explicit.
e timpul reprezentat explicit.
Observăm de asemenea că putem reprezenta un astfel de graf folosind o tabelă unde pe fiecare linie și coloană avem valori/stări posibile ale variabilei/evenimentului care ne interesează. În termeni de știința calculatoarelor orice tabelă bidimensională poate fi foarte ușor reprezentată sub forma unui dicționar având drept cheie o stare posibilă și drept valoare coloana (sau rândul) asociată acesteia, pe care noi o vom reprezenta printr-o listă de asocieri stare-probabilitate.
În Haskell structura de date de tip dicționar se numește Map și se construiește pe baza a două tipuri de date, tipul asociat cheii și cel asociat valorii. Plecând de la cele de mai sus, putem crea un modul pe nume Markov.Chain în care să definim o structură de tip dicționar având proprietățile descrise de noi, după cum urmează:
module Markov.Chain where import Data.Map as M -- Markov Chain: DAG with probabilities on arcs -- also, a dictionary that associates a -- probability to each successor type Chain a = M.Map a [(a, Float)] |
A se nota că am importat Data.Map cu numele M pentru a simplifica folosirea funcțiilor din modul și a structurii de date Map.
Ca o observație, conținutul acestui prim articol mi se pare suficient de abstract și arid încât să îi sperie pe diletanți. Nu vă panicați totuși, de aici încolo încep exemplele, mai exact exemplul, adică aplicația de generat text. Am mai pomenit de câteva ori dadadodo aici, iar întâmplarea face că rezultatul obținut din tutorial va avea exact aceeași funcționalitate. Procesul de dezvoltare va fi explicat pe parcursul mai multor articole, toate astea ilustrând cât de simplu se poate dezvolta o chestie aparent atât de complicată cum e generatorul de text Markov.
Data viitoare vom defini o interfață minimală pentru noua noastră structură de date, interfață pe care mai apoi o vom folosi pentru a rula câteva exemple de lanțuri Markov. Cu ocazia asta vom observa și motivul pentru care meteorologia nu este (încă) o știință exactă.
Post Scriptum: Atât articolele cât și codul sunt disponibile pe github, de unde pot fi descărcate, testate și modificate, fapt pe care autorul (anume eu) îl încurajează din toată inima. După încheierea procesului de dezvoltare – încheiere ce se va concretiza prin publicarea ultimului articol – voi accepta contribuții la proiect indiferent de natura acestora, cât timp le voi considera pozitive.
- Nu văd care-i problema. Scopul meu e acela de a le arăta oamenilor cum să folosească cuțitul, nu să le explic cum ar putea să-l vâre în alți indivizi. [↩]
- Alese la întâmplare sau obținute din niște date statistice. Aici discuția se poate întinde pe parcursul a cărți întregi. Cert e că pot exista, în funcție de sistemul modelat, metode de a obține niște probabilități condiționate fixe. [↩]
Comentariile sunt dezactivate.
Comments
[…] să scriem împreună un generator de text markov (ii) […]