spyked bricks in the wall

să scriem împreună un generator de text markov (iii)

Până acum am povestit despre lanțuri Markov și am găsit un model computațional de reprezentare a acestora, după care am construit pe baza modelului un program care parcurge pseudo-aleator lanțul și întoarce stările parcurse. Am arătat că stările pot diferi de la un apel la altul și că valoarea stării următoare depinde de distribuția de probabilitate formată de stările succesoare. Din fericire generatoarele de numere pseudo-aleatoare din calculatoarele de zi cu zi sunt suficient de bune încât să asigure încadrarea cu o anumită eroare (suficient de mică) în distribuția fiecărei stări.

O abordare mai serioasă a lanțurilor Markov ar presupune parcurgerea unor subiecte destul de aride precum procesele stochastice și distribuțiile de probabilitate. Din nefericire noi nu avem loc aici să intrăm în astfel de subiecte, motiv pentru care abordarea folosită în continuare va fi una așa-zis „intuitivă”, sau mai degrabă o bâjbâială empirică având rolul de a familiariza cititorul cu problema lanțurilor Markov și a generării de text pe baza lor.

Am plecat din capul locului de la premisa că orice generator de text Markov, sau de orice-altceva-Markov, trebuie să plece de la un model, adică de la un lanț Markov. Un exemplu clasic de lanț Markov este „mersul bețivului”, exemplu pe care îl putem ilustra începând cu formula clasică: fie un bețiv mergând pe o cărare. La fiecare moment de timp 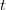, bețivul se poate clătina echiprobabil spre stânga sau spre dreapta cu o distanță oarecare, fixă, indiferent de sensul în care s-a mișcat la momentul anterior de timp. Să se măsoare distanța față de centrul drumului după un număr dat de pași.

Reprezentarea problemei în Haskell este, la fel ca în cazul exemplului cu vremea, de-a dreptul banală. Definim o „direcție” [i] în felul următor:

-- "drunkard" random walk
data Direction = L | R deriving (Eq, Ord, Show)

De asemenea distribuția de probabilitate este definită în enunțul problemei, având forma:

drunkardChain :: Chain Direction
drunkardChain = fromList [
    (L, [(L, 0.5), (R, 0.5)]),
    (R, [(L, 0.5), (R, 0.5)])
    ]

Declarăm și definim în plus o funcție count care pornește de la zero și adună o unitate pentru fiecare pas la stânga și scade o unitate pentru fiecare pas la dreapta:

count :: [Direction] -> Int
count [] = 0
count (L : rest) = 1 + count rest
count (R : rest) = -1 + count rest

Acum nu ne rămâne decât să încărcăm modulul Markov.Examples în GHCi și să apelăm un randomWalk pe drunkardChain, iar rezultatul să îl trimitem către count. Am pus mai jos câteva exemple de rulări:

*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
-2
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
-8
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
-2
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
10
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
-4
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
-6
*Markov.Examples> randomWalk drunkardChain L 50 >>= return . count
0

Observăm că nu avem cum să determinăm în care stâlp sau gard va nimeri bețivul nostru după cincizeci de pași, acesta putând la fel de bine să rămână pe mijlocul drumului până atunci, sau dimpotrivă, să ajungă în casă la Maricela în timp ce stă singură și suspină, mai ceva ca în filme. Modelul poate fi deci considerat o aproximare decentă a realității.

Am pus în Markov.Examples câteva alte modele cu care vă puteți juca. Unul din ele oferă o idee legată de felul în care ar putea arăta un instrument de evaluare a riscurilor pentru domenii cum ar fi asigurările sau medicina. Un alt exemplu, ceva mai abstract, pleacă de la un alfabet format din patru litere și generează un șir de astfel de litere, exemplu care mi se pare că se pretează foarte bine la o abordare non-deterministă asupra limbajelor formale. În fine, ultimul exemplu, pe care l-am denumit sugestiv wordChain, este un dicționar de cuvinte, fiecare cuvânt fiind în plus o stare în lanțul Markov.

Definiția wordChain se prezintă astfel:

-- word succession chain
wordChain :: Chain String
wordChain = fromList [
    ("Ana", [("Ana", 0), ("Ion", 0), ("are", 0.6), ("mananca", 0.3), ("mere", 0.1)]),
    ("Ion", [("Ana", 0), ("Ion", 0), ("are", 0.3), ("mananca", 0.68), ("mere", 0.02)]),
    ("are", [("Ana", 0.01), ("Ion", 0.01), ("are", 0), ("mananca", 0), ("mere", 0.98)]),
    ("mananca", [("Ana", 0.05), ("Ion", 0.05), ("are", 0), ("mananca", 0), ("mere", 0.9)]),
    ("mere", [("Ana", 0.2), ("Ion", 0.2), ("are", 0.25), ("mananca", 0.25), ("mere", 0.1)])
    ]

În urma unei rulări oarecare, obținem ceva în genul:

	*Markov.Examples> randomWalk wordChain "Ana" 12
	["Ana","mananca","mere","Ana","are","mere","are","mere","Ion","mananca","mere","Ion"]

Mașinăria noastră, „plimbătorul aleator”, oferă în acest caz un răspuns la următoarea problemă: plecând de la cuvântul „Ana”, unde, sau mai bine zis prin ce cuvinte mă vor duce mai departe cei doisprezece pași? Alegând cu atenție probabilitățile stărilor următoare, se poate observa că concatenând apoi „drumul” putem obține un soi de înșiruire de cuvinte care chiar are sens. Rezultatele ar trebui să îl convingă până și pe cel mai sceptic dintre noi că lanțul de mai sus ne pune la dispoziție un generator de text Markov cât se poate de cinstit.

Chestia asta e, dacă stăm un pic să cugetăm, de-a dreptul fascinantă, mai ales în perspectiva faptului că teoretic putem să construim un astfel de model cu sute de cuvinte și să îl lăsăm să fie parcurs pentru o perioadă oarecare de timp, de exemplu până în momentul când ajunge să scuipe întreaga operă a lui Shakespeare [ii]. Construirea de mână a unui lanț Markov cu sute de stări este însă dificilă pentru mintea umană, fiind în același timp foarte ușoară o mașină automată, dacă aceasta din urmă este programată de către om.

O soluție la această problemă ar putea fi de exemplu construirea artificială a unui lanț Markov, plecând de la o bază de date formată din cuvinte. Dicționarele de acest fel se găsesc la tot pasul pe web, însă acestea nu ne ajută să scoatem legăturile între cuvinte, adică probabilitatea unui cuvânt de a-l urma pe altul. Ar trebui cumva să scoatem din burtă probabilități; o abordare cât de cât interesantă ar putea consta în aplicarea unor tehnici de NLP mai barbare: împărțirea cuvintelor în părți de propoziție și atribuirea probabilităților în funcție de succesiunea naturală a părților într-o propoziție dată a unei limbi date. Metoda necesită însă cunoștințe serioase de gramatică și în plus nu poate fi implementată ușor în limbi precum germana, unde de exemplu verbul mai sare din când în când la sfârșitul propoziției, cel puțin nu fără unelte specializate pentru procesarea limbajului natural.

Abordarea pe care o văd eu a fi naturală este aceea pe care o face și dadadodo, anume cea a analizei statistice asupra cuvintelor dintr-un text oarecare. O astfel de analiză poate fi oricât de inteligentă, poate să ia în calcul aspectele de mai sus, să țină cont de delimitarea paragrafelor, de punctuație și așa mai departe; noi vom implementa însă varianta „dumb”, care nu face decât să ia o listă de cuvinte și să o analizeze.

Astfel, în articolul următor vom intra în detalii legate de unul sau mai multe feluri în care ar putea fi obținut programatic un lanț Markov dintr-un text oarecare și vom purcede la a implementa un analizor care să ne rezolve problema. Scopul final va fi acela de a îmbina funcționalitățile simulatorului și ale analizorului într-un program care primește la intrare un text oarecare și întoarce un text generat aleator constituit după gusturile cititorului.

1. De fapt sens sau poziție. Îi vom ierta însă autorului această scăpare. [↩]
2. Vedeți teorema maimuțelor infinite. Nu întâmplător m-am inspirat din aceasta pentru a numi aplicația. Sigur, programul nostru își propune să producă rezultate mult mai rafinate, lucrând la nivelul cuvintelor, însă la fel de ușor putem construi un model foarte apropiat de ideea teoremei. De fapt tocmai am ajuns în punctul ăla în care putem face absolut orice ne duce mintea. [↩]