spyked bricks in the wall

să scriem împreună un generator de text markov (iv)

Am stabilit în cadrul părții a treia a seriei că urmează să construim un generator de text Markov format din două componente:

• O componentă care primește la intrare un model statistic, adică un lanț Markov, și întoarce un text generat aleator. Aceasta a constituit subiectul celei de-a doua părți a tutorial-ului.
• O componentă care primește la intrare unul sau mai multe texte într-o limbă oarecare și construiește pe baza lui, respectiv a lor, lanțul Markov necesar generării de text. În cele ce urmează vom implementa această a doua parte, care este de fapt prima parte a algoritmului în totalitatea sa.

Am observat de asemenea că problema construirii unui model pentru generarea propozițiilor într-o limbă oarecare este teoretic intractabilă. Pe de o parte un „corpus al limbii” complet ar putea fi constituit doar din totalitatea textelor și cuvintelor scrise în limba respectivă. Pe de altă parte limba este o unealtă flexibilă, cu reguli și excepții care pot fi încălcate în diverse contexte, și a cărei formalizare este un subiect de cercetare intens la ora actuală în știința lingvisticii.

Prima dificultate este deci cea a timpului și spațiului necesar analizei unui set imens de date, presupunând că avem așa ceva la dispoziție [i]. A doua dificultate este cea a utilizării uneltelor lingvistice actuale, unelte cum ar fi arborii sintactici, a căror construire și parcurgere impune costuri computaționale inerente. Din fericire această a doua dificultate este atacată în cadrul domeniului prelucrării limbajului natural, care însă le vine mai degrabă în ajutor celor ce au apucat să îi parcurgă literatura vastă [ii].

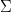
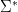
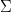
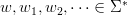
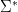
Drept urmare, vom folosi drept model pentru implementarea analizorului nostru următoarea problemă, echivalentă de altfel cu cea a construirii unui lanț Markov pe baza unui text dat. Fie alfabetul latin, extins eventual cu diacritice. Vom nota cu mulțimea șirurilor formate din litere din [iii] și cu cuvinte specifice din . Notăm de asemenea în acest context operația de concatenare a două șiruri cu [iv] și caracterul/cuvântul „spațiu” cu .

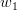
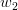
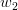
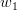
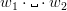
Fiind dat un text oarecare și două cuvinte și , spunem că este succesorul lui dacă în text apare concatenarea .

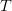
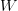
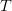
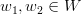
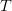
Putem astfel reduce problema la următoarea întrebare: fiind dat un text oarecare și mulțimea de cuvinte asociată lui , care este probabilitatea ca două cuvinte oarecare să se succeadă în ?

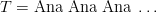
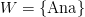
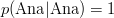
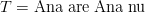
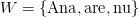
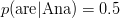
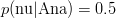
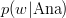
Dacă alegem de exemplu , atunci și modelul rezultat va fi un lanț Markov cu . Dacă alegem în schimb , atunci și și . Generalizând, am putea să modelăm distribuția după cum ne îndeamnă inima, însă din exemplele de mai sus constatăm că distribuția uniformă e o alegere naturală și foarte la îndemână.

Un prim pas al implementării îl reprezintă deci, având la dispoziție textul t — reprezentat în Haskell ca o listă de cuvinte — și un cuvânt w oarecare, obținerea tuturor cuvintelor din t care îi succed lui w:

-- gets all the elements that follow a given element
-- in (or not in) the list
consecutivesOf :: Eq a => a -> [a] -> [a]
consecutivesOf x (x' : x'' : xs)
    | x == x' = x'' : consecutivesOf x (x'' : xs)
    | otherwise = consecutivesOf x (x'' : xs)
consecutivesOf _ _ = []

Observăm că funcția este în fapt destul de generală încât să poată fi aplicată pe variabile de orice tip care asigură comparația la egalitate, fie el String, Char sau Porc. Rezultatele funcției pot fi apoi folosite pentru a calcula distribuția urmașilor unui cuvânt oarecare, sau mai exact numărul de apariții ale fiecărui urmaș în listă:

occurenceList :: Eq a => [a] -> [(a, Int)]
occurenceList xs = zip uniqs $ map (flip countOccurences $ xs) uniqs
    where
    uniqs = nub xs

occurenceList întoarce o listă cu tupluri formate din cuvinte (unice) și numărul lor de apariții în lista inițială. Atât consecutivesOf cât și occurenceList și countOccurences — a cărei implementare nu am pus-o aici — pot fi vizualizate în context în modulul Monkey.Util.Processing al proiectului.

Fiind dat un cuvânt w dintr-un text t oarecare, cele două funcții vor duce practic greul procesării asupra lui w în raport cu t. O observație este aceea că distribuția trebuie normalizată, deoarece tipul Chain a definit mai devreme folosește probabilități reprezentate ca Float-uri subunitare. Funcția normalizeFollowers mapează pe al doilea element al fiecărui tuplu împărțirea la suma tuturor, astfel:

-- convert integers into probabilities
-- by default, states without followers loop into themselves (first equation)
normalizeFollowers :: Eq a => a -> [(a, Int)] -> [(a, Float)]
normalizeFollowers x [] = [(x,1)]
normalizeFollowers _ fs = map (./. total) fs
    where
    total = fromIntegral . sum $ map snd fs
    (x, occ) ./. n = (x, fromIntegral occ / n)

Analiza unui cuvânt decurge astfel natural prin compoziția celor trei funcții definite până acum:

-- given a token and its context, construct a follower-probability
-- model
analyzeToken :: Eq a => a -> [a] -> [(a, Float)]
analyzeToken x = normalizeFollowers x . occurenceList . consecutivesOf x

Având la dispoziție analyzeToken, putem să testăm exemplele de mai sus. Primul exemplu:

*Monkey.Analyzer> analyzeToken "Ana" ["Ana", "Ana", "Ana", "Ana", "Ana"]
[("Ana",1.0)]

rezultă evident într-un lanț Markov format dintr-o singură buclă. Al doilea exemplu:

*Monkey.Analyzer> analyzeToken "Ana" ["Ana", "are", "Ana", "nu"]
[("are",0.5),("nu",0.5)]

dă de asemenea rezultatul așteptat, o distribuție uniformă a celor două cuvinte.

Dorim să mapăm operația peste toate cuvintele unice din text. În plus, dorim să împerechem fiecare cuvânt unic cu distribuția succesorilor săi și să convertim lista obținută într-un lanț Markov, folosind fromList definit în a doua parte a seriei.

-- we assume that a "text" is actually a sequence of tokens
analyze :: (Eq a, Ord a) => [a] -> Chain a
analyze text = fromList $ zip uniqs $ map doAnalyze uniqs
    where
    uniqs = nub text
    doAnalyze = flip analyzeToken $ text

Aplicând analyze — pe care am pus-o în modulul Monkey.Analyzer — pe cel de-al doilea exemplu de mai devreme, obținem:

*Monkey.Analyzer> analyze ["Ana", "are", "Ana", "nu"]
fromList [("Ana",[("are",0.5),("nu",0.5)]),("are",[("Ana",1.0)]),("nu",[("nu",1.0)])]

Propun de asemenea să ilustrăm puterea generatorului pe un exemplu mai interesant:

*Monkey.Analyzer> :m +Markov.Chain 
*Monkey.Analyzer Markov.Chain> words "lungimea medianei corespunzatoare ipotenuzei este egala cu jumatate din lungimea ipotenuzei"
["lungimea","medianei","corespunzatoare","ipotenuzei","este","egala","cu","jumatate","din","lungimea","ipotenuzei"]
*Monkey.Analyzer Markov.Chain> analyze $ words "lungimea medianei corespunzatoare ipotenuzei este egala cu jumatate din lungimea ipotenuzei"
fromList [("corespunzatoare",[("ipotenuzei",1.0)]),("cu",[("jumatate",1.0)]),("din",[("lungimea",1.0)]),("egala",[("cu",1.0)]),("este",[("egala",1.0)]),("ipotenuzei",[("este",1.0)]),("jumatate",[("din",1.0)]),("lungimea",[("medianei",0.5),("ipotenuzei",0.5)]),("medianei",[("corespunzatoare",1.0)])]
*Monkey.Analyzer Markov.Chain> randomWalk (analyze $ words "lungimea medianei corespunzatoare ipotenuzei este egala cu jumatate din lungimea ipotenuzei") "lungimea" 10
["lungimea","ipotenuzei","este","egala","cu","jumatate","din","lungimea","medianei","corespunzatoare"]

Ei, și acum imaginați-vă ce minunății de texte ar putea genera artificial algoritmul (relativ simplu) prezentat până acum dacă am avea la dispoziție niște texte mai mari. Două-trei articole culese la întâmplare de pe Wikipedia s-ar putea dovedi a fi de ajuns pentru a scoate texte dacă nu interesante, atunci măcar amuzante.

Firește că ce am făcut până acum e departe de a fi un program complet. O îmbunătățire importantă ar putea fi adăugarea unui modul principal, care să lege Monkey.Analyzer și Markov.Chain într-un singur program care ia fișiere, le analizează și produce text pe baza lor. O altă îmbunătățire este prelucrarea semnelor de punctuație și a diacriticelor, dat fiind faptul că dorim pe cât posibil să lucrăm doar cu cuvinte. În fine, îmi vin în minte tot felul de mici chestii care ar putea să facă programul mai utilizabil, plus câteva îmbunătățiri mai mari, care probabil că ar face generatorul o idee mai inteligent.

Înainte de a încheia articolul, vă propun două probleme mai mult sau mai puțin interesante, care ar putea da naștere unor fire de dezvoltare ulterioară și eventual unor articole:

• p4.1: Stând un pic și cugetând, mi-am dat seama că reprezentarea probabilităților ca numere în virgulă mobilă nu e așa de utilă pe cât mă așteptam. În primul rând că numerele întregi sunt exacte, în timp ce o operație de împărțire oricât de banală în virgulă mobilă poate genera erori. În al doilea rând, distribuția numerelor fiind discretă și mai ales uniformă, nu își are rostul folosirea împărțirii adiționale mai mult decât raportarea la lungimea listei succesorilor. Sunt curios deci dacă folosirea numerelor întregi în cadrul tipului Chain a rezultă într-o simplificare a codului.
• p4.2: Construirea lanțurilor Markov folosind fromList servește perfect scopului pe care ni l-am propus la începutul seriei. Implementarea poate avea însă probleme de performanță datorate conversiei din liste posibil foarte mari în dicționare, ceea ce denotă în același timp o lipsă de naturalețe a abordării. Doresc astfel să speculez că dicționarele/lanțurile pot fi construite incremental, ceea ce ar reduce analiza la un simplu fold [v]. Mai mult, cred că este posibilă compunerea lanțurilor Markov, deci transformarea întregii povești într-o structură de monoid. Cercetarea acestui aspect ar putea avea implicații serioase din punct de vedere teoretic, putând fi de ajutor de exemplu la examinarea calității unui model în raport cu altul și îmbunătățirea per total a generării de text, fapt care nu a fost tratat în articolele din această serie.

1. Iar Internetul este un astfel de set de date. Apropo de asta, s-ar putea spune că Google este compania care dispune de cele mai sofisticate metode de analiză automată a datelor pe Internet, unde prin date înțelegem inclusiv text scris. Cu alte cuvinte, dacă ar fi putut exista un generator perfect de text într-o limbă anume, probabil ei ar fi fost primii care l-ar fi conceput. [↩]
2. Pomeneam la începutul seriei de utilizarea generatoarelor de text Markov pentru generarea de spam. Am observat, pe marginea comentariilor spam primite pe blog, că adepții acestui fenomen au ajuns să folosească unelte care au un grad destul de mare de sofisticare. Am primit comentarii care păreau de-a dreptul legitime, pentru a afla apoi că acele comentarii erau bucăți de text din alte articole de pe Internet, obținute automat cu ajutorul unor tehnici cum ar fi analiza semantică latentă. [↩]
3. Cu alte cuvinte monoidul liber peste mulțimea . [↩]
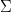
4. În Haskell concatenarea se notează cu operatorul (++). Punctul e folosit mai degrabă pentru a desemna o lege de compoziție în structura algebrică de monoid. [↩]
5. Adică la un catamorfism, care are o semnificație algebrică foarte importantă, pe lângă faptul că ar putea îmbunătăți performanța componentei de analiză. [↩]