spyked bricks in the wall

să scriem împreună un simulator de automate celulare (ii)

Data trecută am discutat câteva aspecte generale legate de automatele celulare și am implementat o funcție care va sta la baza implementării zisului simulator. Aceasta se numește nextCell și întoarce valoarea unei celule după un pas în funcție de valoarea sa și de cea a vecinilor, și în primul rând de numărul care specifică pe scurt regulile de producție ale automatului elementar. Să punem din nou pe foaie signatura funcției:

nextCell :: Elementary -> (Cell, Cell, Cell) -> Cell

Mai departe dorim să extindem această funcționalitate la o așa-zisă „latice”, adică la un șir de celule, pe care noi îl vom reprezenta printr-o listă. Cu alte cuvinte vrem, cunoscând numărul automatului celular, să luăm pe rând fiecare celulă dintr-o listă dată împreună cu vecinii ei la momentul 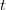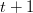și să obținem starea celulei la momentul . Implementarea acestei operații e un pic mai dificilă decât ar părea la o primă vedere, din cauza unor limitări cărora le sunt supuse listele ca model de reprezentare. Să explicăm pe scurt câteva din aceste limitări.

În primul rând e o idee bună să privim la definiția Haskell a tipului de date listă:

data [a] = [] | a : [a]

unde „[]” e lista vidă și „:” e un operator care pune un element de tipul a [i] lângă o listă de elemente având același tip. Definiția este deci dată printr-o recurență de ordinul întâi [ii] la nivelul tipurilor.

O observație ar fi aceea că elementele listei se succed de la stânga spre dreapta, sau de la dreapta spre stânga dacă inversăm parametrii lui „:”. În același timp din definiția automatului celular elementar ne dăm seama că orice celulă are întotdeauna un vecin la dreapta și unul la stânga, ceea ce nu se aplică aici: o listă trebuie cu necesitate să „înceapă” de undeva, adică să aibă un element „cel mai din stânga”. Putem să folosim un tip de date în genul:

data MyLattice a = Void | Lat (MyLattice a) a (MyLattice a)

care ar face implementarea naturală în sensul matematic. Las această abordare drept exercițiu pentru cititor.

Revenind la tipul de date „[a]” și luând în considerare și tipul definit adineauri, o listă poate fi infinită — doar la dreapta în primul caz; atât la stânga cât și la dreapta în al doilea caz — și poate fi reprezentată în acest mod în Haskell. Această situație nu este însă obligatorie, din două motive: unu la mână, noi vom lucra cel mai des cu liste finite, din rațiuni care țin de practică (o listă infinită nu poate fi afișată pe ecran, de exemplu); doi la mână, definiția tipului de date listă e aia de mai sus, iar noi vrem să definim automatul celular pe tot spațiul listelor, nu doar pe cel al listelor infinite.

Din cele menționate mai sus rezultă că trebuie să punem în plus două condiții pe frontieră: una la limita din stânga (primul element al listei), și cealaltă la limita din dreapta. În plus considerăm că nu are sens să tratăm o listă cu un singur element, dat fiind că nu știm dacă e element din stânga, dreapta sau mijloc, pe când cu două elemente putem „completa” cu o celulă liberă în dreapta (sau în stânga, după caz) [iii].

Să numim funcția noastră step și să îi dăm signatura de tip, aproape identică cu a funcției nextCell:

-- Transition function for lattices
step :: Elementary -> [Cell] -> [Cell]

Prima condiție la limită presupune identificarea „primului apel” al funcției și completarea cu o celulă liberă la stânga. Pentru aceasta ne vom folosi de o funcție auxiliară step', care are signatura de tip identică:

step n cells@(l : c : _) = nextCell n (E,l,c) : step' n cells -- boundary

Definim step' în mod similar:

step' :: Elementary -> [Cell] -> [Cell]
step' n (c : r : []) = [nextCell n (c, r, E)] -- boundary
step' n (l : c : r : cells) = nextCell n (l, c, r) : step' n (c : r : cells)
step' _ _ = error "Not enough cells to chew on"

Amintesc faptul că definiția poate părea ușor greoaie, motiv pentru care recomand să vă rezervați câteva momente pentru a o digera, eventual schimbând chestii și observând rezultatele. După o analiză atentă se poate observa că step face exact ceea ce explicam mai devreme: grupează fiecare celulă cu vecinii ei și apelează nextCell, atașând apoi noua celulă restului obținut prin apel recursiv. Apelul însă primește vechea stare a celulei curente ca parametru și o aruncă la gunoi după ce a folosit-o. Un exercițiu bun (și nu tocmai ușor) ar fi găsirea unei forme mai expresive și mai eficiente pentru funcție [iv].

Nu întâmplător signatura funcției step a fost aleasă pentru a utiliza abilitatea Haskell-ului de a lucra cu funcții în formă curry [v]: putem defini automatul celular prezentat în „dinamica traficului” folosind o construcție în genul:

rule184 :: [Cell] -> [Cell]
rule184 = step 184

Observăm că trimiterea numărului 184 ca argument transformă vechea funcție într-o nouă funcție care primește ca argument o listă de celule și scuipă la ieșire o nouă listă de celule, care reprezintă starea automatului la pasul următor de timp. Putem itera pașii la infinit folosind funcția iterate, care are signatura de tip:

iterate :: (a -> a) -> a -> [a]

al doilea argument fiind starea de plecare. Putem de asemenea să personalizăm funcția, legând variabila de tip a la Cell:

runCell1D :: ([Cell] -> [Cell]) -> [Cell] -> [[Cell]]
runCell1D = iterate

Pentru a nu ne zgâi prea tare la liste (ba chiar la liste de liste), propun să afișăm fiecare latice ca pe o linie orizontală cu „x”-uri și „.”-uri și pe verticală să trasăm evoluția în timp. Funcția printCells face tocmai asta:

-- Pretty print cells
printCells :: [[Cell]] -> IO ()
printCells = mapM\_ $ printRow
    where
    printRow r = mapM_ (putStr . show) r >> putStrLn ""

Nu există suficient loc aici pentru a explica monadele, deci mă rezum la a vă spune că printCells folosește mapM_, o variantă monadică a map-ului funcțional, care întoarce liste de tipul (), care e un fel de void funcțional. Funcția printRow face același lucru, apelând întâi show pentru a converti Cell în String și afișând celula cu putStr. La finalul fiecărei latice e pusă o linie nouă, folosind putStrLn cu argument șirul vid. Nu există semantic nici o diferență între construcția de mai sus și două for-uri imbricate din C.

Mai rămâne să dăm niște exemple de stări inițiale:

-- Examples
-- Make our cellular lattices finite (we want to terminate)
exampleLat :: [Cell]
exampleLat = take 40 $ F : iterate id E
 
exampleLat2 :: [Cell]
exampleLat2 = take 40 $ E : iterate inv E
    where
    inv F = E
    inv E = F

Primul exemplu conține o singură celulă „plină” la stânga. Al doilea exemplu e mai puțin fascinant pentru regula 184, deci nu îl vom prezenta aici. Vom rula însă folosind GHCi două reguli, 184 și 60, folosind exampleLat ca intrare.

Regula 184 (primii 20 de pași):

*Cell1D> printCells $ take 40 $ runCell1D rule184 exampleLat
x.......................................
.x......................................
..x.....................................
...x....................................
....x...................................
.....x..................................
......x.................................
.......x................................
........x...............................
.........x..............................
..........x.............................
...........x............................
............x...........................
.............x..........................
..............x.........................
...............x........................
................x.......................
.................x......................
..................x.....................
...................x....................

Regula 60 (primii 32 de pași):

*Cell1D> printCells $ take 32 $ runCell1D rule60 exampleLat
x.......................................
xx......................................
x.x.....................................
xxxx....................................
x...x...................................
xx..xx..................................
x.x.x.x.................................
xxxxxxxx................................
x.......x...............................
xx......xx..............................
x.x.....x.x.............................
xxxx....xxxx............................
x...x...x...x...........................
xx..xx..xx..xx..........................
x.x.x.x.x.x.x.x.........................
xxxxxxxxxxxxxxxx........................
x...............x.......................
xx..............xx......................
x.x.............x.x.....................
xxxx............xxxx....................
x...x...........x...x...................
xx..xx..........xx..xx..................
x.x.x.x.........x.x.x.x.................
xxxxxxxx........xxxxxxxx................
x.......x.......x.......x...............
xx......xx......xx......xx..............
x.x.....x.x.....x.x.....x.x.............
xxxx....xxxx....xxxx....xxxx............
x...x...x...x...x...x...x...x...........
xx..xx..xx..xx..xx..xx..xx..xx..........
x.x.x.x.x.x.x.x.x.x.x.x.x.x.x.x.........
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx........

Prima rulare reprezintă o mașinuță plimbându-se pe o stradă liberă. A doua e ceva mai interesantă, reprezentând un triunghi Sierpinski care-i fractal de felul lui, deci se poate succede prin auto-similaritate într-o veselie. Regula 184 am observat însă că nu prezintă nimic special când pleacă de la stări inițiale banale, motiv pentru care vom defini o stare inițială aleatoare, folosind două funcții din System.Random, newStdGen (care întoarce un generator de „obiecte” aleatoare) și randoms (care întoarce o listă de „obiecte” aleatoare):

exampleLat3 :: IO [Cell]
exampleLat3 = newStdGen >>= return . take 40 . randoms

Observăm că deja nu mai putem scăpa de monada IO, care folosește generatorul de numere aleatoare din sistemul de operare. Să încercăm să compilăm exemplul:

[1 of 1] Compiling Cell1D           ( Cell1D.hs, interpreted )
 
Cell1D.hs:86:48:
    No instance for (Random Cell)
        arising from a use of `randoms'
    Possible fix: add an instance declaration for (Random Cell)
    In the second argument of `(.)', namely `randoms'
    In the second argument of `(.)', namely `take 40 . randoms'
    In the second argument of `(>>=)', namely
        `return . take 40 . randoms'
Failed, modules loaded: none.

Să derivăm deci de mână o instanță pentru clasa de tipuri Random pentru Cell, lucru care în cazul nostru vă asigur că e de-a dreptul banal dacă ne uităm la definiția clasei Random.

-- Cells can be randomized
-- Note: "ranges" of cells are ignored
instance Random Cell where
    random g
        | n `mod` 2 == 0 = (E, g')
        | otherwise = (F, g')
        where
        (n, g') = next g
    randomR _ = random

Tot ce face definirea funcției random e să ia un număr n și un generator g' din aplicarea funcției next și să aplice asupra lui o distribuție uniformă, verificând dacă numărul pseudo-aleator e divizibil cu 2 sau nu. În funcție de asta, random întoarce un dublet compus din E sau F și noul generator. Dat fiind că nu avem de-a face cu domenii de valori, definiția lui randomR e identică.

Să rulăm din nou regula 184 cu 30 de pași pe noua stare inițială:

*Cell1D> exampleLat3 >>= printCells  . take 30 . (runCell1D rule184)
x....xxx.xx.xx.x.xxxx.xx......xxxxxxxxx.
.x...xx.xx.xx.x.xxxx.xx.x.....xxxxxxxx.x
..x..x.xx.xx.x.xxxx.xx.x.x....xxxxxxx.x.
...x..xx.xx.x.xxxx.xx.x.x.x...xxxxxx.x.x
....x.x.xx.x.xxxx.xx.x.x.x.x..xxxxx.x.x.
.....x.xx.x.xxxx.xx.x.x.x.x.x.xxxx.x.x.x
......xx.x.xxxx.xx.x.x.x.x.x.xxxx.x.x.x.
......x.x.xxxx.xx.x.x.x.x.x.xxxx.x.x.x.x
.......x.xxxx.xx.x.x.x.x.x.xxxx.x.x.x.x.
........xxxx.xx.x.x.x.x.x.xxxx.x.x.x.x.x
........xxx.xx.x.x.x.x.x.xxxx.x.x.x.x.x.
........xx.xx.x.x.x.x.x.xxxx.x.x.x.x.x.x
........x.xx.x.x.x.x.x.xxxx.x.x.x.x.x.x.
.........xx.x.x.x.x.x.xxxx.x.x.x.x.x.x.x
.........x.x.x.x.x.x.xxxx.x.x.x.x.x.x.x.
..........x.x.x.x.x.xxxx.x.x.x.x.x.x.x.x
...........x.x.x.x.xxxx.x.x.x.x.x.x.x.x.
............x.x.x.xxxx.x.x.x.x.x.x.x.x.x
.............x.x.xxxx.x.x.x.x.x.x.x.x.x.
..............x.xxxx.x.x.x.x.x.x.x.x.x.x
...............xxxx.x.x.x.x.x.x.x.x.x.x.
...............xxx.x.x.x.x.x.x.x.x.x.x.x
...............xx.x.x.x.x.x.x.x.x.x.x.x.
...............x.x.x.x.x.x.x.x.x.x.x.x.x
................x.x.x.x.x.x.x.x.x.x.x.x.
.................x.x.x.x.x.x.x.x.x.x.x.x
..................x.x.x.x.x.x.x.x.x.x.x.
...................x.x.x.x.x.x.x.x.x.x.x
....................x.x.x.x.x.x.x.x.x.x.
.....................x.x.x.x.x.x.x.x.x.x

Exemplul ăsta e cu adevărat interesant de observat pe latice mai mari, eventual mult mai mari decât cea prezentată aici. Dacă privim laticea ca pe un drum populat cu mașini care merg înspre dreapta pe o singură bandă, putem privi și șirurile adiacente de celule ca pe ambuteiaje. Observăm că ambuteiajele se mută spre stânga în timp și că spre sfârșit mașinile converg spre o distribuție uniformă [vi]. În final viteza maximă (o celulă per pas) e atinsă prin lăsarea a cel puțin unei celule libere față de automobilul din față.

… presupunând că nu există intersecții care să poată provoca ambuteiaje, fapt care e în sine demn de studiat. Las însă și acest exercițiu pe seama cititorului, în caz că nu are răbdare să aștepte până cândva în viitor. Următorul articol se va concentra cel mai probabil pe studiul unor metode de vizualizare marginal mai sofisticate decât modul text, care deși în cazul de față s-a dovedit a fi foarte util, nu e și cel mai plăcut ochiului. Până atunci vă invit să dați o privire peste fișierul sursă Haskell cu simulatorul și să îl comparați cu implementarea proprie, implementare pe care vă recomand să o faceți cu articolul în față înainte să vă uitați peste codul din fișier.

1. Cu mențiunea că a e de fapt o variabilă de tip, motiv pentru care putem defini liste de întregi ([Int]), de valori booleene ([Bool]) și de orice alt tip, aceasta fiind la urma urmei întreaga rațiune din spatele polimorfismului. [↩]
2. Despre care trebuie să fi auzit cândva în liceu, la studierea șirurilor. [↩]
3. Iată deci că automatul celular nu poate fi totuși definit pe întreg spațiul listelor, ceea ce înseamnă că nu putem lucra pur funcțional. Ne obișnuim cu ideea și trecem mai departe. [↩]
4. Ar putea fi de folos în acest sens tipul MyLattice a definit mai sus și observația că acesta este inerent comonadic. V-ar putea ajuta și faptul că există deja explicații de-a gata pe Internet, pe care însă va trebui să le găsiți singuri dacă aveți de gând să rezolvați exercițiul. [↩]
5. Care nu are nimic de-a face cu prepararea alimentului curry, ci cu matematicianul Haskell Curry, de unde își trage numele și limbajul. [↩]
6. Fapt ce nu-i musai să fie adevărat dacă starea inițială provine dintr-o altă distribuție. Exercițiu pentru cititori: generați starea inițială dintr-o distribuție normală și reveniți cu un răspuns și eventual un grafic. Sunt chiar curios cum evoluează automatul în acest caz. [↩]