spyked bricks in the wall

naturalețea în matematici

Începem scurta noastră – căci nu-mi aparține mie personal mai mult decât aparține oricărui individ care a dat cu privirea peste știința matematicii măcar o dată în viața sa – sinteză cu o precizare: în caz că vă întrebați ce treabă ar putea avea naturalețea cu matematica, mă ofer să vă lămuresc, deși sunt de părere că ar fi trebuit să vă lămuriți și singuri până acum, iar dacă sunteți ceva mai tineri nu-i vremea pierdută. Matematica nu-i o chestiune așa, pur abstractă, sau dacă este, atunci nu-i degeaba în felul respectiv. Orice, dar absolut orice structură matematică are un corespondent mai mult sau mai puțin direct în lumea reală.

Se face că lumea reală, așa cum o priviți, auziți și toate cele, conține structuri – în sensul pur algebric al cuvântului – care pot fi naturale sau nu, opusul fiind poate „nenaturale”, sau „artificiale” în funcție de context. Naturalul face în general referire la ceva preexistent, care e într-un anumit fel din capul locului, ori în contextul nostru matematic sensul e o idee diferit: „natural” înseamnă mai degrabă „imediat” sau „intuitiv”, adică un sens și/sau o formă care se mapează direct pe mintea umană și mecanismele sale. Ideea e valabilă însă și în zisa „lume reală”, care e într-un fel anume în virtutea faptului că așa e percepută dânsa, individul neavând un punct clar de reper legat de un alt fel în care ar putea fi aceasta.

Particularitatea interesantă a matematicii este însă aceea că se prezintă drept o unealtă adresată exclusiv minții – ca și filosofia, de altfel. Acest aspect este cel care trimite mințile mai puțin norocite către judecăți greșite precum aceea că algebra e un nonsens abstract sau cea care spune că statistica-i o știință invalidă, că „Dumnezeu nu joacă barbut” [i]. Altfel naturalețea e prezentă peste tot în matematici, ceea ce face din acestea o disciplină după care individul trebuie să-și formeze mintea și nu invers [ii], fapt validat la o adică de istoria îndelungată a matematicii.

Exemplul cel mai banal de naturalețe este cel al mulțimilor: se iau niște obiecte și se pun într-o oală și gata-i mulțimea. După care s-au luat „numerele” și s-a constituit „mulțimea numerelor”, care fiind expresia naturală a o serie de lucruri cât și o chestie care ilustrează niște limite axiomatice, s-au dovedit a fi suficient de naturale încât mulțimea în cauză să se numească cea a numerelor naturale, adică 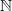[iii]. Abia apoi s-au gândit matematicienii la operatori și operații, adică adunări, înmulțiri, exponențieri, tetrări și ce o mai fi după, chestii care s-au integrat perfect cu monoizi, grupuri, inele, câmpuri, spații vectoriale, latice, algebre și câte și mai câte, unul mai „abstract” ca altul.

O altă chestie „naturală” din matematică e logaritmul natural, ceea ce poate părea pe bună dreptate extrem de ciudat. Funcția e cel puțin dubioasă, dat fiind faptul că-i legată de numărul , ăla de-a dreptul transcedental, la fel ca 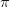– ba chiar cele două sunt legate între ele, ambele având de-a face cu cercurili. Din formula lui Euler aflăm și că 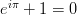, care-i o identitate de o frumusețe neasemuită pentru matematicieni și în fine, la rândul ei naturală. Totuși motivul pentru care logaritmul natural se cheamă „natural” ține în totalitate de domeniul analizei. În primul rând că este expresia unei sume infinite [iv] și poate și mai intuitiv e faptul că aceeași constantă se poate exprima și printr-o limită, pe care probabil că ați studiat-o în liceu, iar dacă nu, o veți studia poate (sau nu, după caz). Mai amuzant e însă aspectul următor: definiția limitei și respectiv a seriei creează o legătură intrinsecă între fundamentele analizei și algebra diferențială, motiv pentru care calculul derivatelor ajunge foarte des să dea rezultate care mai conțin un la numitor sau la numărător. Astfel matematicienii (sau fizicienii) au constatat că mai bine folosesc ei logaritmul în bază , care pare a fi chiar „natural” cumva în sistemul dat, și cu asta basta.

În fine, poate cel mai bun exemplu de naturalețe a matematicii se regăsește în – ați ghicit, iar de nu să nu fiți surprinși! – teoria categoriilor. Categoria este însăși o structură naturală, și în plus există o lege doar parțial scrisă care zice că orice structură bazată pe categorii – fie ea functor sau F-algebră sau morfism functorial – fie e naturală, fie nu-i deloc. Ba chiar morfismele functoriale – care-s fix morfisme între functori, după cum le zice numele – sunt denumite în literatura de specialitate și transformări naturale, pentru că nu există transformare între doi functori care să nu fie naturală, iar dacă ar fi nu i-ar zice transformare naturală. Aici „naturalul” tinde chiar către sensul de „naturalețe”, aparent paradoxal: unde s-a mai văzut ca într-un domeniu atât de abstract mai toate demonstrațiile să fie imediate, ba chiar unele din ele banale și o mare parte exprimate direct în definiții?

Ba chiar „naturalețea” transformării naturale e intrinsecă într-un fel atât de intrinsec încât orice-i natural în matematică trebuie să aibă corespondent în teoria categoriilor – de exemplu matricele și functorii. Iară numerele naturale și principiul inducției sunt de fapt expresii naturale ale catamorfismului, care-i așa, un fel de banană; derivata poate că e și dânsa un functor – n-am verificat, dar poate, cine știe -, la fel cum sunt și logicile modale, la fel cum sunt și proiectele software. Și uite așa aflăm că naturalețea asta de fapt leagă chestii între care nu există nici o legătură aparentă, dar în fapt există. Și cu ocazia asta aflăm și că matematica e frumoasă, ba chiar are și sâni.

1. Vai, dar m-am luat de Einstein, cum mi-am permis acest lucru?! Săriți vă rog și umpleți-mă de căcat, da’ înainte de asta țineți vă rog cont de faptul binecunoscut în mediul științific că fizicianul nostru genial a fost la urma urmei un matematician mediocru. Asta sigur că nu-i neagă cu nimic meritele, da’ tot domniile voastre care aruncă cu rahat ar trebui să cunoască faptele – tot binecunoscute în mediile academice – că spațiile 4D au fost descoperite de Minkowski și Poincaré, iar geometria hiperbolică de Bolyai și Lobacevski.

   Deci aproape că am putea spune – dacă am fi răi – că Einstein a adus contribuții mult mai notabile în fizica cuantică decât în relativitate. Ceea ce este chiar aproape adevărat dacă ne amintim de exemplu de condensatul Bose-Einstein, care nu-i așa aclamat ca 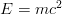, cum nu e nici efectul fotoelectric. [↩]

2. Sigur, depinde în ce sens decurge procedeul cu pricina. Dacă sensul e acela al chinului înspre înțelegere, atunci toate-s bune și frumoase. Pe de altă parte dacă Gheorghe se chinuie în stil Coreean să învețe pe de rost „formule”, efortul îl va transforma într-o enciclopedie de formule matematice, chit că după aia Gheorghe al nostru nu mai e bun de nimic altceva pe lumea asta. [↩]
3. Apoi s-a descoperit că există o relație între numerele naturale și mașinile Turing, după care – sau înainte? nu contează – a fost formulat principiul inducției și așa mai departe, un natural după celălalt. [↩]
4. Exercițiu: căutați pe Google și documentați-vă. Loazelor, acu’ nu v-oi da eu totul pe tavă. [↩]