naturalețea în matematici
duminică, 19 aug. 2012, 19:34
Începem scurta noastră – căci nu-mi aparține mie personal mai mult decât aparține oricărui individ care a dat cu privirea peste știința matematicii măcar o dată în viața sa – sinteză cu o precizare: în caz că vă întrebați ce treabă ar putea avea naturalețea cu matematica, mă ofer să vă lămuresc, deși sunt de părere că ar fi trebuit să vă lămuriți și singuri până acum, iar dacă sunteți ceva mai tineri nu-i vremea pierdută. Matematica nu-i o chestiune așa, pur abstractă, sau dacă este, atunci nu-i degeaba în felul respectiv. Orice, dar absolut orice structură matematică are un corespondent mai mult sau mai puțin direct în lumea reală.
Se face că lumea reală, așa cum o priviți, auziți și toate cele, conține structuri – în sensul pur algebric al cuvântului – care pot fi naturale sau nu, opusul fiind poate „nenaturale”, sau „artificiale” în funcție de context. Naturalul face în general referire la ceva preexistent, care e într-un anumit fel din capul locului, ori în contextul nostru matematic sensul e o idee diferit: „natural” înseamnă mai degrabă „imediat” sau „intuitiv”, adică un sens și/sau o formă care se mapează direct pe mintea umană și mecanismele sale. Ideea e valabilă însă și în zisa „lume reală”, care e într-un fel anume în virtutea faptului că așa e percepută dânsa, individul neavând un punct clar de reper legat de un alt fel în care ar putea fi aceasta. (mai mult…)
cu cofunctori și matrice inversabile
duminică, 19 feb. 2012, 15:37
Articolul despre atom ne-a lăsat în pom cu o particularitate destul de neplăcută (și care dă spre inconsistență) a sistemului prezentat: toate reprezentările abstracte din cadrul acestuia sunt cu precădere duale, deci binare [i], pe când abordarea categorială e una ternară. Cu alte cuvinte, categoria ca construcție naturală a matematicii e formată din obiecte (notate de obicei 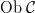
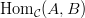

Definiția o generalizează pe cea a monoidului, care-i în fapt și la urma urmei o categorie cu un singur obiect care-i de fapt o mulțime 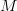 , ale cărei elemente sunt săgeți în categoria dată, iar compunerea e operația binară de compunere a monoidului. Definiția generală a monoidului dă de fapt un triplet format dintr-un obiect și două morfisme, într-un mod analog cu monadele, dar astea nu-s legate de discuția noastră. (mai mult…)
, ale cărei elemente sunt săgeți în categoria dată, iar compunerea e operația binară de compunere a monoidului. Definiția generală a monoidului dă de fapt un triplet format dintr-un obiect și două morfisme, într-un mod analog cu monadele, dar astea nu-s legate de discuția noastră. (mai mult…)
- Și iată cum am comis și erezia de a folosi numere în cadrul unor teorii care fac abstracție de acestea la un nivel fundamental. [↩]
- Mai exact asociativitatea operației și existența unui element neutru [↩]