cu cofunctori și matrice inversabile
duminică, 19 feb. 2012, 15:37
Articolul despre atom ne-a lăsat în pom cu o particularitate destul de neplăcută (și care dă spre inconsistență) a sistemului prezentat: toate reprezentările abstracte din cadrul acestuia sunt cu precădere duale, deci binare [i], pe când abordarea categorială e una ternară. Cu alte cuvinte, categoria ca construcție naturală a matematicii e formată din obiecte (notate de obicei 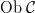
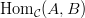

Definiția o generalizează pe cea a monoidului, care-i în fapt și la urma urmei o categorie cu un singur obiect care-i de fapt o mulțime 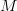 , ale cărei elemente sunt săgeți în categoria dată, iar compunerea e operația binară de compunere a monoidului. Definiția generală a monoidului dă de fapt un triplet format dintr-un obiect și două morfisme, într-un mod analog cu monadele, dar astea nu-s legate de discuția noastră. (mai mult…)
, ale cărei elemente sunt săgeți în categoria dată, iar compunerea e operația binară de compunere a monoidului. Definiția generală a monoidului dă de fapt un triplet format dintr-un obiect și două morfisme, într-un mod analog cu monadele, dar astea nu-s legate de discuția noastră. (mai mult…)
- Și iată cum am comis și erezia de a folosi numere în cadrul unor teorii care fac abstracție de acestea la un nivel fundamental. [↩]
- Mai exact asociativitatea operației și existența unui element neutru [↩]