un argument împotriva închipuitei fragmentări a ecosistemului android

sâmbătă, 17 nov. 2012, 12:35

Acest articol poate fi considerat o prelungire a breviarului istoric ARM, în mare pentru că ilustrează cu mai multe amănunte implicațiile pe care le aduce varietatea dispozitivelor și platformelor bazate pe arhitectura ARM. După cum bine știm deja, problemele software-ului se mapează de multe ori unu la unu pe cele ale hardware-ului de dedesubt, motiv pentru care argumentul va fi extins la proiectul care face cel mai bine uz de această varietate, și anume sistemul de operare Android [i].

Zisul argument vine împotriva tuturor gurilor rele care susțin sus și tare că „Android e un mediu fragmentat”, spre deosebire de iOS-ul de la Apple care nu este și nici nu are cum să fie, dat fiind că vine într-o unică varietate pe o unică platformă hardware (plus minus una-două), bazată tot pe ARM. Cititorul se poate lămuri în legătură cu problema printr-o căutare pe Google după „android fragmentation”, care întoarce literalmente sute de rezultate relevante. Sigur, așa-zisa fragmentare s-ar putea să fi fost o problemă pe versiunile 2.x de Android [ii], însă clar nu se mai poate vorbi despre așa ceva la nivelul Android 4.x, pentru că vedeți în continuare. (mai mult…)

  1. În mod normal câștigătorul ar trebui să fie mediul GNU/Linux, care însă consider că are mari lacune la nivelul portării interfețelor cu utilizatorul și a altor aplicații posibil dependente de arhitectură. [↩]
  2. Care într-un mod ironic acoperă cea mai mare parte a dispozitivelor mobile cu Android de pe piață la ora actuală. Chestia o să devină istorie într-un timp foarte scurt, dacă nu luăm în calcul chinezăriile foarte ieftine, ci doar pe cele suficient de fiabile. [↩]

să scriem împreună un simulator de automate celulare (ii)

duminică, 4 nov. 2012, 14:17

Data trecută am discutat câteva aspecte generale legate de automatele celulare și am implementat o funcție care va sta la baza implementării zisului simulator. Aceasta se numește nextCell și întoarce valoarea unei celule după un pas în funcție de valoarea sa și de cea a vecinilor, și în primul rând de numărul care specifică pe scurt regulile de producție ale automatului elementar. Să punem din nou pe foaie signatura funcției:

nextCell :: Elementary -> (Cell, Cell, Cell) -> Cell

Mai departe dorim să extindem această funcționalitate la o așa-zisă „latice”, adică la un șir de celule, pe care noi îl vom reprezenta printr-o listă. Cu alte cuvinte vrem, cunoscând numărul automatului celular, să luăm pe rând fiecare celulă dintr-o listă dată împreună cu vecinii ei la momentul 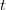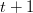t și să obținem starea celulei la momentul t + 1. Implementarea acestei operații e un pic mai dificilă decât ar părea la o primă vedere, din cauza unor limitări cărora le sunt supuse listele ca model de reprezentare. Să explicăm pe scurt câteva din aceste limitări. (mai mult…)

brick quote #13

luni, 29 oct. 2012, 23:00

All around me darkness gathers,
Fading is the sun that shone,
We must speak of other matters,
You can be me when I’m gone

Flowers gathered in the morning,
Afternoon they blossom on,
Still are withered in the evening,
You can be me when I’m gone.

  • Neil Gaiman, The Sandman, Vol. 9: The Kindly Ones

despre statistică: distribuții.

sâmbătă, 27 oct. 2012, 18:43

Statistica este domeniul care studiază folosirea unor volume (cât mai mari, sau mai bine zis cât mai generale cu putință) de date spre a extrage ceva util din acestea. Definiția „utilului” diferă de obicei de la o aplicație la alta: în fizică ne poate da o intuiție asupra felului în care se deplasează lichidele sau electronii; în biologie poate explica evoluția anumitor caracteristici ale speciilor; în medicină poate corela evoluția unei boli cu anumiți factori din viața pacientului; în inteligența artificială raționamentul statistic e o metodă de inferență și așa mai departe. Toate acestea au însă un numitor comun.

Am stabilit mai demult că nu e de ajuns să avem date, trebuie să și știm cum să le folosim. Un set de date oarecare e dat de una sau mai multe variabile, cum ar fi de exemplu populația unui oraș măsurată la intervale egale de timp. Variabila din exemplu poate să crească sau să scadă de la momentul 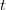t la momentul t + \delta t; nu știm cu certitudine în care direcție o ia, motiv pentru care o numim variabilă aleatoare. În plus, mărimea intervalului \delta t e relevantă. De la o zi la alta pot muri zece oameni și se pot naște trei, sau invers. De la o lună la alta atât sporul negativ cât și cel pozitiv cresc, nu știm exact cu cât. Dar dacă luăm evoluția din ultima sută de ani a populației Pământului, pe perioade de cinci ani? Știm exact că per total a crescut.

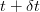
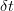
Dacă ați făcut liceul, atunci cu siguranță că vă aduceți aminte că la analiza matematică tendința funcțiilor de a scădea sau de a crește putea fi studiată cu ajutorul derivatelor. Ei, derivata asta, precum și inversa ei, integrala, se dovedește a fi extrem de utilă în algebra probabilităților [i]: putem afirma că există o funcție care exprimă evoluția probabilistică a unei variabile aleatoare, pe care o vom numi densitate de probabilitate. Din aceasta poate fi calculată, printr-o sumă sau o integrală, o distribuție cumulativă, care dă probabilitatea ca variabila aleatoare să se afle într-un interval dat. Și așa am ajuns și la cuvântul cheie „distribuție”. (mai mult…)

  1. Care pleacă de la spații boreliene și axiome ale lui Kolmogorov și în fine, trece prin teoria mulțimilor și ajunge la chestii care ne depășesc pe noi ăștia care nu suntem experți într-ale matematicilor. Ne limităm la a spune că algebra și analiza matematică sunt foarte utile pentru statistică și probabilități și e bine să aveți o idee despre ele, chit că poate n-o să le aplicați niciodată direct. [↩]

să scriem împreună un simulator de automate celulare (i)

duminică, 14 oct. 2012, 12:06

Automatele celulare au reprezentat o noutate prin anii ’40-’60, la momentul descoperirii lor de către Ulan și von Neumann. În anii ’70-’80 conceptul a devenit iarăși un subiect de interes datorită cercetărilor (mai degrabă empirice) făcute de Stephen Wolfram și alții pentru a reprezenta și studia diverse trăznăi precum modele ale fizicii digitale sau ale vieții. În anii 1990-2010 descoperirile în cadrul domeniului merg într-un ritm lent, însă nu încetează a se ivi. Cu toate acestea automatele celulare rămân o unealtă educațională extrem de utilă, dată fiind puterea de reprezentare care stă la baza lor. Am arătat deja cum putem modela cu ajutorul acestora un fenomen comun prezent în natură și în mediile sociale, ne mai rămâne doar să punem în practică conceptele prezentate.

Pentru a putea atinge scopul articolului, acela de a construi un simulator de automate celulare, avem nevoie de unelte ajutătoare. Acestea pot fi după caz plăci de textolit, tranzistoare, lămpi, ansambluri hidraulice sau piese LEGO; va trebui însă să mă credeți pe cuvânt că cea mai simplă cale de a implementa un automat celular este scrierea unui program, orice astfel de mașinărie teoretică fiind echivalentă cu cel puțin un subset al unui automat Turing. Din motive în principal egoiste, dar și pentru că doresc să împing mintea cititorului într-un anumit șablon de gândire, aleg să scriu programul care simulează automate celulare în Haskell; nu în C, Python, Java, Ruby sau ce alte fetișuri mai au programatorii în ziua de astăzi, ci într-un limbaj funcțional, care poate transpune în mod natural concepte matematice elementare precum funcțiile în construcții care mai apoi vor rula pe calculator.

Există deci câteva motive pentru care merită să parcurgeți articolul de față și pe cele ce-i vor urma: (mai mult…)

« Articole mai vechi
Articole mai noi »