despre statistică: distribuții.
sâmbătă, 27 oct. 2012, 18:43
Statistica este domeniul care studiază folosirea unor volume (cât mai mari, sau mai bine zis cât mai generale cu putință) de date spre a extrage ceva util din acestea. Definiția „utilului” diferă de obicei de la o aplicație la alta: în fizică ne poate da o intuiție asupra felului în care se deplasează lichidele sau electronii; în biologie poate explica evoluția anumitor caracteristici ale speciilor; în medicină poate corela evoluția unei boli cu anumiți factori din viața pacientului; în inteligența artificială raționamentul statistic e o metodă de inferență și așa mai departe. Toate acestea au însă un numitor comun.
Am stabilit mai demult că nu e de ajuns să avem date, trebuie să și știm cum să le folosim. Un set de date oarecare e dat de una sau mai multe variabile, cum ar fi de exemplu populația unui oraș măsurată la intervale egale de timp. Variabila din exemplu poate să crească sau să scadă de la momentul 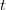
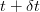
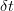
Dacă ați făcut liceul, atunci cu siguranță că vă aduceți aminte că la analiza matematică tendința funcțiilor de a scădea sau de a crește putea fi studiată cu ajutorul derivatelor. Ei, derivata asta, precum și inversa ei, integrala, se dovedește a fi extrem de utilă în algebra probabilităților [i]: putem afirma că există o funcție care exprimă evoluția probabilistică a unei variabile aleatoare, pe care o vom numi densitate de probabilitate. Din aceasta poate fi calculată, printr-o sumă sau o integrală, o distribuție cumulativă, care dă probabilitatea ca variabila aleatoare să se afle într-un interval dat. Și așa am ajuns și la cuvântul cheie „distribuție”.
O distribuție este, cităm:
DISTRIBÚȚIE s. f. 1. distribuire; repartiție. ◊ felul cum sunt repartizate rolurile unei piese, ale unui film etc.; totalitatea actorilor dintr-o piesă de teatru, dintr-un film etc. 2. (fiz.) modul cum sunt repartizate elementele mai multor mulțimi (electroni, atomi, molecule) după valorile posibile ale unei mărimi caracteristice (viteză, energie etc.). 3. dirijarea și repartizarea spre consumatori a unui fluid, flux de energie etc.
Academia română ne oferă, după cum bine ne-am obișnuit, o pseudo-definiție, adică o definiție particulară, incompletă, compusă din sub-definiții [ii]. Motiv pentru care recurgem la a căuta o definiție pentru englezescul „distribution”, la Princeton de exemplu:
S: (n) distribution, statistical distribution ([statistics] an arrangement of values of a variable showing their observed or theoretical frequency of occurrence)
Distribuția este deci o funcție construită din date obținute prin observație sau pe baza unor teorii, sau mai bine zis un model construit din acestea. Ori a construi un model înseamnă a abstractiza, a obține o formă, deci a exprima ceva anume cu precizie optimă. Pentru că ar fi necesar spațiul unei cărți pentru a da exemple practice cu distribuții și toate cele — care exemple deja există în cărți consacrate de fizică, biologie, economie, învățare automată etc. –, mă voi rezuma la a prezenta trei distribuții statistice clasice: uniformă, binomială și normală.
a. distribuția uniformă
Distribuția uniformă nu-i astfel în sensul îmbrăcăminții cu același nume, ci în sensul în care valorile sunt distribuite în mod egal într-un spațiu dat de valori. Cu alte cuvinte dacă am la dispoziție o mulțime de trei valori posibile, eu pot la fel de probabil să obțin prima valoare, pe a doua sau pe a treia. Probabilitatea de a obține o valoare dată în distribuția uniformă cu 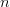
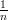
Cazul continuu scoate la iveală o densitate de probabilitate care nu-i nimic altceva decât o dreaptă orizontală, și cum în general în lumea numerelor reale lucrăm cu intervale de valori, probabilitatea de a ne situa într-un interval e dată de capetele intervalului. Distribuția este deci în sine banală, însă are aplicații la tot pasul.
Un exemplu des întâlnit al distribuției uniforme este acela al monedei, adică al zarului cu două fețe. Pentru a genera artificial o lovitură sau un „miss” într-un joc de role-playing dat — Fallout, să zicem –, calculatorul „dă cu banul”, sau „dă cu zarul”, folosind la bază surse de evenimente mai mult sau mai puțin aleatoare din lumea reală cum ar fi bătăile în taste sau mișcările mouse-ului, plus niște algoritmi. Algoritmii în cauză sunt puși acolo tocmai pentru a asigura „corectitudinea generatorului”, adică faptul că valoarea obținută se încadrează într-o distribuție anume [iii], în acest caz în distribuția uniformă.
Același principiu se aplică la generarea cheilor criptografice, fișierelor temporare, mutărilor la ceva joc de poker și probabil și în cazul BSOD-urilor din Windows. Dacă aveți o colecție imensă de filme porno și nu știți la care să vă uitați, puteți scrie (ca exercițiu) în doi timpi și trei mișcări un script care să aleagă la întâmplare un fișier pe care apoi să-l dea ca argument player-ului de filme.
b. distribuția binomială
Revenind la exemplul cu „hit versus miss” din Fallout, putem modela efectiv acest fenomen de reușită/eșec printr-o distribuție teoretică. Să zicem că probabilitatea de a lovi adversarul într-o situație [iv] dată e 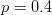
Dacă probabilitatea ca o lovitură să reușească e 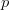
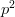
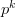
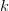
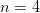
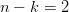
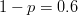
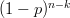
Ca urmare, probabilitatea ca exact două lovituri din patru să reușească și restul să eșueze este 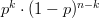
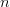
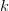
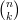
O observație ar fi aceea că distribuția binomială funcționează doar pentru variabile aleatoare binare, generalizarea părând o idee mai scârboasă pentru ochiul neobișnuit cu notațiile matematice. Din fericire lumea se tot învârte în jurul chestiilor binare, așa că nu-i mare problemă.
c. distribuția normală
Cunoscută în vulg și drept „curba lui Gauss”, distribuția normală e „normală” în sensul în care are un rol standard în cadrul domeniului statisticii. Variabilele aleatoare admit în general calculul unei valori medii („mean”) și a unei „abateri” („deviation”), adică a unei diferențe între medie și valoare. Dacă media e intuitivă, o abatere standard e ceva mai greu de digerat, reprezentând media unei distribuții pătratice care depinde de media distribuției inițiale și de valorile variabilei aleatoare.
Cele două metrici expun însă două aspecte în egală măsură intuitive: pe de o parte media unui set de valori — de exemplu media notelor dintr-un an — este un 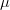
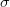
În ceea ce privește reprezentarea grafică, vârful curbei lui Gauss reprezintă valoarea mediei, în timp ce lățimea clopotului determină valoarea abaterii standard, care delimitează astfel regiuni pe suprafața acestuia. Funcția pare să dea oarecum spre universalitate în domeniul statisticii, fiind folosită inclusiv la exprimarea altor distribuții. Practic cam orice chestie incertă poate fi modelată folosind distribuții gaussiene, rezultatele fiind mai mult sau mai puțin reușite din punct de vedere calitativ. Cert e că volumele „cât mai mari” de date tind să se încadreze într-o distribuție normală, fapt care-i remarcabil atât pentru natură cât și pentru statistica matematică.
Pe lângă aceasta și cele două din urmă mai există câteva distribuții interesante și care ar merita studiate: Bernoulli, Student t, Chi, Dirichlet.
- Care pleacă de la spații boreliene și axiome ale lui Kolmogorov și în fine, trece prin teoria mulțimilor și ajunge la chestii care ne depășesc pe noi ăștia care nu suntem experți într-ale matematicilor. Ne limităm la a spune că algebra și analiza matematică sunt foarte utile pentru statistică și probabilități și e bine să aveți o idee despre ele, chit că poate n-o să le aplicați niciodată direct. [↩]
- Pe pagina din link se găsește și un set de definiții care variază în funcție de domeniu, set care e mult prea lung și plictisitor pentru a fi menționat în articol. [↩]
- Cu un anumit grad de încredere. Bunăoară, calculați probabilitatea ca în urma unei aruncări, un zar să se oprească pe o muchie oarecare. Evenimentul e extrem de improbabil, însă nu imposibil, muchiile zarului nefiind perfecte. [↩]
- Adică cu o anumită armă, de la o anumită distanță, în funcție de atributele personajului, de momentul zilei și de bonusurile/penalizările de armură și agilitate ale adversarului, plus o doză de noroc pur. Cam ăștia sunt factorii care determină reușita unui atac în RPG-ul mediu, în caz că sunteți curioși. Acum calculatoarele fac în spate toate chestiile astea, fapt ce nu se aplică la un joc „pen and paper” cum ar fi Dungeons & Dragons. [↩]
- Consecutive sau nu, dat fiind că loviturile sunt independente. Să simplificăm, ignorând cazul unui „critical miss” care poate duce la penalizări adiționale și alte asemenea briz-briz-uri care fac jocul mai interesant, din motivul că dorim să rămânem în contextul distribuției binomiale. [↩]
Comentariile sunt dezactivate.
Comments
[…] e să ia un număr n și un generator g' din aplicarea funcției next și să aplice asupra lui o distribuție uniformă, verificând dacă numărul pseudo-aleator e divizibil cu 2 sau nu. În funcție de asta, random […]
[…] de exemplu un program care să cunoască un măr într-o imagine oarecare prin alcătuirea unui model statistic și testarea acestuia folosind exemple pozitive și negative […]