cu poli și copiat
miercuri, 5 sept. 2012, 23:57
N-am mai abordat de ceva vreme subiectul, deci să reluăm: Mihai scrie despre un student care cere lucrări pe o listă de discuții oarecare, pe marginea unei materii oarecare din facultate. Cele două (lista și materia) sunt prea puțin relevante; e importantă însă observația că este vorba despre o disciplină de master, unde participanții sunt deja ingineri, adică oameni cu capul pe umeri și toate cele. Ei, ți-ai găsit. Lăsând la o parte faptul că trebuie să fii naiv — să nu zic altfel — să cumperi lucrări pe liste publice, în văzul lumii, problema copiatului aduce iar discuții pro și contra [i], care se rezumă în final la starea „sistemului” [ii], care-i așa și pe dincolo, adică putrezit!
Drept să o spun, și eu sunt student la master și pot să spun că programul nu s-a ridicat pe deplin la așteptările mele. Un argument care îmi invalidează dezamăgirea ar fi acela că la Politehnică-ACS (secția calculatoare) mai toate materiile faine sunt înghesuite în ultimii doi ani de licență, astfel că la master se fac în mare parte subiecte ce țin pur de specializare, nu cum se face la UT Cluj sau prin alte părți — ba chiar la multe facultăți dinafară, pentru că argumentul „dacă-i dinafară e musai mai bine ca la noi” e foarte popular. Totuși un lucru e clar: mulți titulari nu își organizează la fel de bine cursurile la master în raport cu cele de licență, pentru că mulți sunt ocupați cu altele și au mai degrabă așteptări de implicare din partea studenților. Stilul nu-i unul deosebit, ba ar fi chiar interesant dacă unele materii nu ar fi atât de plictisitoare. (mai mult…)
- Păi cum, nu știți? românul s-a născut filosof. Ce contează că nu suntem în stare să lucrăm cu algebre și categorii, noi discutăm probleme profunde de etică, alea. Ce contează regulamentele la care am aderat încă de când am semnat foaia de înscriere? „Dăle-n măsa”, noi suntem mai presus de toate prostiile astea. [↩]
- De parcă oamenii ar fi familiari cu teoria sistemelor; haha, ce glumă bună. [↩]
naturalețea în matematici
duminică, 19 aug. 2012, 19:34
Începem scurta noastră – căci nu-mi aparține mie personal mai mult decât aparține oricărui individ care a dat cu privirea peste știința matematicii măcar o dată în viața sa – sinteză cu o precizare: în caz că vă întrebați ce treabă ar putea avea naturalețea cu matematica, mă ofer să vă lămuresc, deși sunt de părere că ar fi trebuit să vă lămuriți și singuri până acum, iar dacă sunteți ceva mai tineri nu-i vremea pierdută. Matematica nu-i o chestiune așa, pur abstractă, sau dacă este, atunci nu-i degeaba în felul respectiv. Orice, dar absolut orice structură matematică are un corespondent mai mult sau mai puțin direct în lumea reală.
Se face că lumea reală, așa cum o priviți, auziți și toate cele, conține structuri – în sensul pur algebric al cuvântului – care pot fi naturale sau nu, opusul fiind poate „nenaturale”, sau „artificiale” în funcție de context. Naturalul face în general referire la ceva preexistent, care e într-un anumit fel din capul locului, ori în contextul nostru matematic sensul e o idee diferit: „natural” înseamnă mai degrabă „imediat” sau „intuitiv”, adică un sens și/sau o formă care se mapează direct pe mintea umană și mecanismele sale. Ideea e valabilă însă și în zisa „lume reală”, care e într-un fel anume în virtutea faptului că așa e percepută dânsa, individul neavând un punct clar de reper legat de un alt fel în care ar putea fi aceasta. (mai mult…)
o introducere ușor neobișnuită în domeniul arhitecturii software
duminică, 29 iul. 2012, 16:24
Arhitectura, sau mai general proiectarea chestiilor este un subdomeniu al ingineriei ca oricare altul, care se ocupă, am putea spune lipsiți de rigoare, cu descrierea chestiilor în cauză. Bunăoară, dacă doresc, inginer fiind, să proiectez un ciocan spre a rezolva o problemă dată (de obicei bătutul cuielor), va trebui – dat fiind că-s om, iară nu orice om, ci inginer – să îmi formulez un set de cerințe și întrebări adiacente acesteia, legate printre altele de: părțile componente ale ciocanului, felul în care arată acestea, din ce sunt formate și cum se îmbină ele spre a forma mai mult decât suma părților lor.
Fundamentele acestei paradigme sunt aceleași în cazul sistemelor software, motiv pentru care și există în prezent acest domeniu oarecum bizar al ingineriei programelor pe calculator [i]. Diavolul se regăsește bineînțeles în detalii, acolo unde teoreticienii încearcă să prezică evoluția software-ului în timp. Dacă în cazul unui ciocan lucrurile stau destul de simplu – dai cu el până se strică -, software-ul evoluează destul de haotic în timp, degradându-se și pierzându-și din fiabilitate în moduri greu de prevăzut. Colac peste pupăză, inginerii noștri plini de creativitate gândesc modele și implementări care de care mai complexe, când rolul abstractizării e tocmai opusul, anume acela de a simplifica lucrurile. Deci aici zic că ar ajuta un pic să luăm lucrurile de la zero, deci să regândim problema. (mai mult…)
- Da, dragi cititori, ingineria software e un ceva anume extrem de bizar prin felul ei de a fi. Aceasta ba apare în, ba dispare din mintea inginerului programator, existând și în același timp încetând să existe pentru acesta la un moment dat. Fenomenul se datorează nu numai faptului că lumea ideilor e volatilă în cadrul unui singur individ, ci și aceluia că oameni diferiți pot privi o singură problemă în moduri complet disjuncte, ajungând astfel să petreacă o perioadă considerabilă de timp stabilindu-și un limbaj comun. Astfel au apărut hack-uri imense dezvoltate de oameni cu interese profund diferite, cum e nucleul Linux, și astfel au luat viață inclusiv unele produse ale consumului de LSD, cum e Unix. [↩]
cu cofunctori și matrice inversabile
duminică, 19 feb. 2012, 15:37
Articolul despre atom ne-a lăsat în pom cu o particularitate destul de neplăcută (și care dă spre inconsistență) a sistemului prezentat: toate reprezentările abstracte din cadrul acestuia sunt cu precădere duale, deci binare [i], pe când abordarea categorială e una ternară. Cu alte cuvinte, categoria ca construcție naturală a matematicii e formată din obiecte (notate de obicei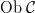 
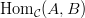
Definiția o generalizează pe cea a monoidului, care-i în fapt și la urma urmei o categorie cu un singur obiect care-i de fapt o mulțime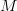 
, ale cărei elemente sunt săgeți în categoria dată, iar compunerea e operația binară de compunere a monoidului. Definiția generală a monoidului dă de fapt un triplet format dintr-un obiect și două morfisme, într-un mod analog cu monadele, dar astea nu-s legate de discuția noastră. (mai mult…)
- Și iată cum am comis și erezia de a folosi numere în cadrul unor teorii care fac abstracție de acestea la un nivel fundamental. [↩]
- Mai exact asociativitatea operației și existența unui element neutru [↩]