spyked bricks in the wall

despre dragoste [§]

Dacă acum ceva (destul de mult) timp am dorit să găsesc o formulă aproximativ filosofică a acestui fenomen care, țin să precizez, încă mi se pare extrem de dubios și cât se poate de diabolic, voi încerca astăzi o abordare implicită, formală [§], pur matematică, așa cum îi șade bine acestei trăiri minunate, care într-o lume perfectă este musai să fie una, evident, perfectă (foarte perfectă, după cum probabil ar spune primarul și prietenul nostru mult iubit, Marean).

Voi defini obiectul inefabilei mele iubiri, denumit sugestiv She (adicătelea ea), ca fiind cea care mă iubește, deci prin propoziția „She Loves Me”:

module Shelovesmenot where
 
data She = She Loves Me deriving (Show, Eq)
data Loves = Loves deriving (Show, Eq)
data Me = Me deriving (Show, Eq)

Cu toate acestea, eu, cel îndrăgostit, sunt, după cum explicam în prima parte, extrem de confuz și niciodată sigur pe dragostea mea, sentimentul de nesiguranță ducându-se asimptotic către „1” logic, mai ceva ca regimul tranzitoriu al unui inversor CMOS. Clar, pe Ea o aplicăm iubirii, de unde rezultă o funcție care se aplică pe Me, subiectul. Dar din cauza nesiguranței, „She Loves Me” devine un tuplu (She, Not), în virtutea negativismului manifestat de către îndrăgostit.

De asemenea, dat fiind faptul că trăim într-o lume perfectă, ea mă iubește sau nu mă iubește, deci nu vom accepta o altă logică decât cea de ordinul I (deși atenție, în lumea reală lucrurile de cele mai multe ori nu stau tocmai așa). Vorba aia, într-o lume perfectă până și CMOS-ul are regimul tranzitoriu așa de bine conturat încât te lovește din „0” în „1” și invers când te aștepți mai puțin (sau după un 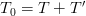, unde 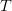e durata nivelului „1” și 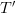cea a nivelului „0”). Așadar, constructorul lui Not este:

data Not = Indeed | Not deriving (Show, Eq)

În acest moment, îndrăgostitul nostru, Me, se poate apuca să rupă petale de flori în lumea sa matematică și nu în cea reală (un gest destul de eco-friendly). Vom ignora motivele pentru care amorezul și-a ales acest context și această modalitate de a-și petrece timpul (în timpul ăsta putea să facă altceva, cum ar fi să își scoată iubirea la un film sau să o ducă în Banbu). Probabil că e peste măsură de îndrăgostit, sau poate că doar a consumat prea multe ciuperci/prafuri/pastile/ierburi, sau poate pur și simplu suferă de bipolar disorder, caz în care, într-o lume plină de imperfecțiuni cum e a noastră, funcția nu i s-ar mai termina, computațional vorbind, deci kaput la băiatu’. În cea perfectă nu ne interesează dacă se termină sau nu.

Până una alta, vom avea nevoie de o funcție de complementare a stării lui Me:

compl :: Not -> Not
compl x
	| x == Indeed = Not
	| otherwise = Indeed

și de o funcție care să itereze la infinit tuplul (She, Not) între „da, nebuna mă iubește” și „nu, matracuca nu mă iubește”, adică (She Loves Me, Indeed) respectiv (She Loves Me, Not):

lovesme :: (She,Not) -> [(She,Not)]
lovesme (She Loves Me, x) = (She Loves Me, x) :
	(lovesme (She Loves Me, compl x))

Iar acum presupunem că Me se apucă să rupă toate petalele, sepalele și alte elemente reproducătoare ale plantei (adică o apucă de bijuterii). Numărul de petale ale unei flori poate varia lejer după șirul lui Fibonacci, dar vom presupune pur întâmplător că nebunul are o floare cu opt petale [ii]:

*Shelovesmenot> last $ take 8 $ lovesme (She Loves Me, Indeed)
(She Loves Me,Not)

Better luck next time, Me.

[§] – Abordarea este, între noi fie vorba, una doar aproximativ formală, dar destul de apropiată de „the true shit”. Autorul a ales să se exprime în Haskell atât datorită acestui atu al limbajului, cât și pentru că limbajul își evaluează parametrii într-un mod al naibii de leneș, iar în cazul ăsta eu vreau să fie leneș, altfel nu ar funcționa. De asemenea, am folosit limbajul mai sus menționat fiindcă vreau să dau dureri de cap celor care nu-s acomodați cu programarea funcțională, la urma urmei de ce aș suferi doar eu.

[ii] – Și fiindcă ăsta este punctul culminant al poveștii, voi explica și celor haskell-illiterate ce se întâmplă aici: funcția lovesme numără „she loves me indeed, she loves me not, …” la infinit, deci întoarce o listă infinită de astfel de aberații. Cum floarea mea are opt petale, eu iau doar primele opt elemente ale listei cu take și, cum primele șapte elemente oricum sunt degeaba, îl aleg direct pe ultimul, folosind last. Tristul rezultat este cel pe care îl vedeți, iar de nu mă credeți convingeți-vă, nu-i magie neagră.