spyked bricks in the wall

despre statistică: numere mari.

Dacă matematica e o știință naturală într-un sens anume, atunci putem spune că statistica este acea ramură a matematicii care e cea mai apropiată de concret, adică de natură în sensul ei propriu. E chiar atât de apropiată încât am putea comite eroarea de a rupe statistica de domeniul matematicii și a o introduce bine mersi în alte științe care dispun de dânsa. Legătura e de fapt atât de strânsă încât practicarea științei ar fi imposibilă dacă nu am avea la dispoziție o unealtă atât de utilă cum este statistica. Mai mult, nu am exagera deloc spunând că necesitatea se extinde de la nivelul științei-scientia către cel al științei-knowledge, adică în toate epistemele posibile și imposibile.

Cuvântul „statistică” a fost aparent „coined” [i] de un individ pe nume Gottfried Achenwall, un prusac care a căutat să eficientizeze funcționarea statului prin diverse metode, scriind câteva lucrări notabile [ii] pe temă. Una din lucrări [iii] menționează termenul „statistik” cu referire la afacerile statului și în particular la colectarea și organizarea datelor numerice în cadrul acestuia. De aici și motivul pentru care nu putem vorbi despre date fără a ne gândi la statistică, și vice versa.

Privind problema din alte puncte de vedere, cum ar fi cel al inteligenței artificiale, statistica e un mod de a raționa, la fel ca deducția, care la rândul ei reprezintă o întreagă familie de așa-zise „metode de inferență”. Raționamentul inductiv are atât avantaje cât și dezavantaje față de cel deductiv: de exemplu îmi e foarte ușor să afirm că „toți câinii sunt animale”, pe baza faptului că nu am observat până în prezent vreun câine care să nu fie animal. Pe de altă parte nu pot să trag concluzia că „toate florile sunt galbene” dacă de exemplu eu am observat doar flori galbene pe parcursul existenței mele ca observator, la fel cum nu pot afirma că „Pământul se încălzește” doar pe baza faptului că vara asta a fost mai călduroasă decât cea de acum zece ani.

Constatăm deci că statistica se ocupă cu studiul datelor și cu extragerea unor concluzii pe baza acestora. De asemenea constatăm că concluziile trase pot fi eronate într-o anumită măsură, motiv pentru care aceeași statistică își propune să impună rigori referitoare la analiza datelor. Bunăoară dacă într-un grup de zece persoane nouă ascultă un anumit gen de muzică, asta nu e o dovadă clară în sensul afirmației că genul respectiv este popular în cadrul unui grup extins de persoane. Similar, dacă eu îmi propun să iau autobuzul cu o oră mai târziu „pentru că atunci este mai liber”, argumentul poate fi valid sau nu, în funcție de factorii introduși în problemă [iv].

Un principiu important al științei, care se regăsește cu vârf și îndesat și în statistică, este acela că orice experiment trebuie să poată fi reprodus, principiul stând la baza însăși metodei științifice. Astfel omul de știință, sau poate simplul observator, poate valida o teorie prin simplă observație, presupunând că observația este valabilă într-un cadru cât mai general — deci mai degrabă într-un grup de o mie de persoane decât într-unul de zece. Într-o lume ideală am putea să afirmăm despre o proprietate anume a acesteia (a lumii) că este universală: dacă ne limităm la universul vizibil, atunci mecanica relativistă e universală; dacă ne limităm la lumea cuantică, atunci mecanica cuantică e universală etc. De exemplu dacă arunc o piatră în câmpul gravitațional al Pământului, deși probabilitatea ca aceasta să rămână în aer plutind nu e musai zero, statistic e extrem de improbabil ca evenimentul să se producă în câteva miliarde de ani de acum — aspect de altfel fundamental în ceea ce privește aplicarea metodelor statistice în fizică.

Această abordare a dus la formularea unei teoreme care poartă numele de „legea numerelor mari”, care spune că dacă un experiment e repetat de un număr suficient de mare (ideal infinit) de ori cu un rezultat anume, atunci rezultatul respectiv trebuie să fie valid. În practică „suficient de mare” e un număr care depinde de numărul de stări ale sistemului, adică de cantitatea de informație pe care sistemul o furnizează observatorului [v]. De exemplu în cazul unui joc de rock-paper-scissors există 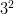, adică nouă stări posibile, aceasta decurgând din numărul de participanți distincți (doi) și numărul de semne (trei). În cadrul unui sistem economic oarecare atât numărul de participanți cât și numărul de mutări posibile sunt mult mai mari, deci vă las pe voi să faceți calculul. Același raționament se aplică în cazurile vreme versus climă, celule versus oameni etc. [vi].

A se nota însă că explicațiile de mai sus sunt aproximative. Statistica este un domeniu mult mai variat de atât și are la bază o serie de concepte teoretice tari, printre care se numără analiza matematică și probabilitățile. Un TL;DR al textului ar suna ceva în genul „statistica e aia pe care o folosești când ai date din care vrei să extragi șabloane”, însă lucrurile nu stau chiar atât de simplu. Din această cauză voi mai scrie pe temă, chit că nu cunosc atât de bine domeniul încât să îl pot trata exhaustiv. Doresc însă ca această serie să fie un ghid pentru persoanele care n-au răbdare să pună mâna pe carte, scris în speranța că va ajunge să cultive această rabdare; pentru că nu pot să concep om civilizat care să nu aibă un minim de cunoștințe legate de subiect.

1. Cuvânt pentru care nu există sinonim în română. [↩]
2. Staatsverfassung der Europäischen Reiche im Grundrisse, 1752. [↩]
3. Vorbereitung zur Staatswissenschaft, 1748. [↩]
4. Un astfel de raționament poate îmbina logica și statistica. De exemplu „majoritatea oamenilor din Rucubești termină munca până în ora 18 seara” (date care pot fi verificate) și „în ultimele două săptămâni am plecat de la muncă la ora 20 seara și a fost mai liber” (date pur inductive) implică împreună că într-adevăr la ora 20 autobuzul e mai liber decât la 18.

   E relevantă de asemenea observația că indivizii „raționali” se bazează pe ambele metode de inferență. Pe de altă parte „raționamentul” pur inductiv, dacă putem să-i spunem raționament, e prezent și la animale, acest fapt fiind confirmat de experimentul cu câinele lui Pavlov. [↩]

5. Deci de mărimea numită entropie. [↩]
6. De fapt multe sisteme au comportament similar atât la nivel macro cât și la nivel micro, complexitatea fiind în acest caz doar o iluzie. Aspectul face obiectul de studiu al cărții „A New Kind of Science” a lui Stephen Wolfram, subiectul fiind legat de fractali, complexitate, teoria haosului, alea. [↩]