spyked bricks in the wall

dinamica traficului, un model

DEX dă termenului de trafic o definiție particulară și cvasi-improprie:

TRAFÍC, traficuri, s. n. 1. Totalitatea transporturilor de mărfuri sau de persoane care se fac pe o anumită cale de comunicație, cu anumite mijloace de transport, într-un interval de timp și în condiții precizate. ♦ Totalitatea legăturilor de telecomunicație stabilite într-un anumit interval de timp și în anumite condiții tehnice.

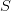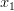
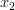
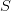În fapt traficul este sinonim cu conceptul abstract de transport, care presupune un spațiu al cărui obiect (nu neapărat unicul) poate fi mutat de la un punct către un alt punct . Mutarea va duce astfel la transformarea lui într-un alt spațiu, tot 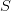, însă cu poziția lui schimbată [i]. Ținând cont de faptul că două obiecte distincte nu pot ocupa aceeași poziție la un moment dat – sau, dacă ar fi să ne luăm după definiție, în același spațiu dat -, dorim să modelăm transportul unei mulțimi (posibil infinite) de obiecte prin .

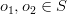
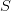Complexitatea deloc redusă a problemei prezentate mai sus mă obligă să îi aduc simplificări acesteia din urmă. Cazul particular ilustrativ în acest sens este o găselniță a unor matematicieni și calculatoriști celebri – printre care se numără și John von Neumann -, anume automatul celular – mai cu seamă cel unidimensional, ale cărui proprietăți le voi enunța în cele ce urmează.

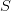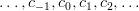
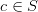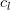
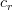
Fie un șir – posibil infinit – de celule , deci o mulțime peste care există o relație de ordine totală pe care nu o vom numi aici. Fiind dată o celulă oarecare , pot fi deci determinate imediat „celula din stânga” și „celula din dreapta în raport cu . Ideea de „stânga” și „dreapta” poate fi generalizată la distanțe arbitrare față de o celulă dată, însă pentru simplitate vom considera că fiecare celulă își cunoaște doar vecinii din stânga și din dreapta.

Fiind dată o celulă oarecare 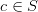, poate avea la un moment dat una din două stări posibile: „liberă” și „ocupată”. Notăm celula „liberă” cu 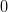și pe cea „ocupată” cu 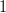și definim (printr-un ușor abuz de notație) o funcție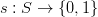 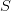care asociază fiecărei celule din „valoarea” sau starea ei la un moment dat. Observăm două aspecte importante:

• Starea, sau „valoarea” celulei nu este o proprietate inerentă acesteia, ci obiectului care (posibil) o populează. Puteam la fel de bine să definesc un codomeniu cu o singură stare – caz destul de neinteresant – sau cu trei, patru sau o infinitate de stări – fapt ce ar fi crescut considerabil complexitatea reprezentării. Motivația alegerii a fix două valori posibile este aceea că mapează în mod natural modelul pe cel al atomului.
• Șirul de mai sus începe să se asemene extrem de mult cu un vector ordinar de biți. Acest fapt vine cu unele implicații, pe care le vom menționa mai târziu.

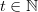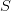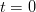În fine, dorim să imprimăm o dinamică sistemului de mai sus, să îl facem să evolueze în timp, motiv pentru care vom defini o măsură numită „timp”, împreună cu o variabilă reprezentând momentul curent de timp. Valorile și [ii] la momentul sunt cunoscute. 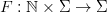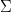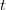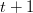În cazul cel mai general ar trebui să cunoaștem și forma unei funcții – unde este mulțimea funcțiilor – care, primind ca argumente momentul curent de timp și o funcție , să stabilească forma funcției la momentul [iii]. Adineauri am presupus însă că o celulă dată își „cunoaște” doar vecinii din stânga și din dreapta, motiv pentru care putem lucra sub simplificarea că valoarea imediat următoare a unei celule depinde doar de valoarea sa anterioară și de valorile anterioare ale vecinilor din stânga și din dreapta.

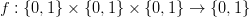
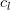
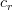
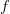Definim astfel o funcție , care are următoarea semnificație: fiind date, pentru un oarecare, valorile la un moment dat ale lui , și în această ordine, întoarce valoarea lui la momentul imediat următor. Constatăm că 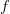este invariantă, nefiind dependentă de 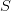; deci nu depinde de poziția celulelor, ducând în mod implicit la determinarea formei lui la momentul 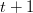, ținând cont de respectarea ipotezei simplificatoare de mai sus – aceea că celulele nu depind în mod arbitrar unele de altele.

Forma funcției 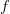ne permite de asemenea să lucrăm foarte ușor cu șiruri de biți. Dat fiind faptul că 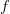primește drept argument un 3-tuplu de biți, numărul de valori posibile pe care le poate lua acesta este 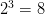. În plus, putem reprezenta funcția sub forma unei tabele de adevăr. O convenție în domeniul automatelor celulare unidimensionale este aceea a reprezentării funcției sub forma unui număr pe opt biți. De exemplu automatul celular 42 are semnificația în binar a șirului de biți 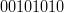, care șir se referă la valorile lui 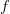, după cum urmează: bit-ul cel mai din dreapta este cel mai nesemnificativ bit, deci are asociat index-ul zero, adică argumentul 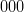. Bitul imediat următor (de la dreapta la stânga) e bitul unu, deci 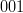, apoi doi (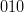) și așa mai departe, până la bitul 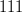. Există deci în total 256 de automate celulare 1D binare posibile.

După această lungă introducere, definiția automatului celular modelator de trafic devine banală: acesta are asociat numărul 184 și este recunoscut pentru capacitatea sa de a simula (printre altele) dinamica traficului, chestie pe care o vom analiza și noi imediat. Regulile care definesc automatul celular 184 sunt următoarele:

• (r0) 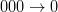– șoseaua liberă rămâne liberă.
• (r1) 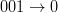– idem (r0).
• (r2) 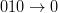– obiectul care are liber în dreapta va elibera celula curentă.
• (r3) 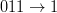– invers față de (r2), obiectul care nu are liber în dreapta va rămâne pe loc.
• (r4) 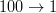– obiectul din stânga care găsește celula curentă liberă o va ocupa.
• (r5) 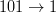– idem (r4).
• (r6) 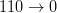– idem (r2).
• (r7) 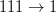– idem (r3).

Astfel obținem un automat foarte simplu care simulează fluxul traficului printr-o „țeavă” (discretă). Acestea fiind date, putem începe să analizăm comportamentul modelului în raport cu diverse situații inițiale, să observăm cum se comportă acesta în funcție de cardinalitatea șirului de celule sau am putea chiar să îmbunătățim modelul pentru a trata cazuri mai complicate legate de dinamica traficului. De exemplu în traficul auto o bună parte din ambuteiaje sunt cauzate de proasta funcționare sau proiectare a intersecțiilor, astfel că putem să gândim un sistem de „intersecții” bazat pe modelul dat mai sus. Bineînțeles, putem face toate astea într-un articol viitor.

1. A se observa că definiția face complet abstracție de natura spațiului sau a obiectelor aflate într-însul. La urma urmei nu ne interesează dacă avem de-a face cu vaci, saci de făină sau biți, elementele ce țin de detaliu – cum ar fi de exemplu un protocol de transport – fiind lăsate în totalitate implementării. [↩]
2. E totuși impropriu spus că are o „valoare”. Mai degrabă este definit printr-o expresie care se schimbă în timp. [↩]
3. De fapt dacă facem abstracție de argumentul asociat timpului, putem spune că 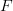este o funcțională, adică un functor. [↩]