spyked bricks in the wall

importanța purității în semantică

În cadrul articolului despre semantică am discutat despre cum aceasta e o componentă esențială a limbajului. Reluând, putem afirma că semantica ajută la conceptualizarea obiectelor concrete și implicit la abstractizare, stabilind în același timp și convenții [i]. De asemenea, am afirmat că într-un sistem format dintr-un număr suficient de mare de persoane admitem existența inconsistențelor de reprezentare a conceptelor. Acestea pot exista dintr-o serie de motive precum acela că oamenii sunt în sinea lor diferiți sau că ajung să asimileze concepte în moduri diferite.

În plus, există o serie de aspecte legate mai mult sau mai puțin de limbaj, aspecte care afectează semantica acestuia. Poate fi vorba de proprietăți de bază ale limbajului [ii] sau de calități emergente, pe care creatorul limbajului vrea sau nu să le imprime acestuia, dar a căror existență necesită demonstrații non-triviale. În această ultimă categorie intră și puritatea. Pentru a face un compromis între rigurozitate și intuiție, voi defini conceptul de puritate în termeni care combină matematica cu calculatoarele.

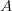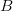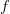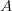Să presupunem că avem două obiecte, și . Să mai presupunem că putem trage o săgeată de la la 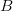(putem nota 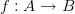, notație identică cu aceea a funcțiilor matematice), săgeată care are semnificația unui proces de calcul. Putem astfel spune că săgeata 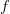trece obiectul 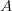în obiectul 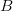sau că 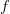este un calcul care ia 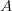și are ca efect .

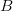Fiind date 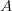, , 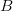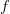ca mai sus, spunem că 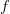este pură dacă și numai dacă 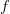are în mod strict pe 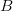ca efect. Cu alte cuvinte, oricare ar fi obiectul 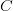, , 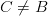atunci 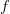nu are ca efect 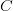. În caz contrar, spunem că 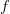are efecte laterale.

Exemple tipice de calcule pure sunt morfismele din teoria categoriilor [iii], sau și mai concret funcțiile matematice. Din punct de vedere matematic, orice funcție 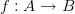are o semantică clară: pentru o valoare dată din mulțimea 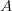, 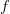definește asocierea unei unice valori din 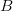. Funcția noastră nu mai „execută” nici un fel de acțiuni care să afecteze alte entități din universul dat – ba chiar, prin definiția formală, universul problemei este format doar din cele două mulțimi și un morfism -, astfel că e practic imposibilă apariția ambiguităților semantice.

Calculele cu efecte laterale sunt în schimb omniprezente în programele pe calculator. Un program care calculează o funcție afișând apoi rezultatul pe ecran are efecte laterale, deoarece programul are atât un efect principal, adică rezultatul întors de funcție, cât și unul lateral, mai exact livrarea rezultatului către un flux de octeți care reprezintă terminalul unde va fi afișat rezultatul. Exemplul cel mai elocvent de program C al cărei funcție f are efecte laterale este următorul:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

int a = 0;
int f(int x)
{
    a++;
    return x;
}
 
int main(void)
{
    printf("a = %d\n", a);
    printf("f(1) = %d\n",f(1));
    printf("a = %d\n", a);
    printf("f(1) = %d\n",f(1));
 
    return 0;
}

Observăm că, deși din punct de vedere matematic aici f are rol de funcție identitate, ea are un efect lateral care constă în incrementarea valorii variabilei globale a. A doua observație este că deși f este o funcție prin definiție corectă (va fi parsată și compilată corect), ea poate avea efecte laterale neprevizibile dacă de exemplu este apelată în paralel de două fire de execuție.

În limbajul natural, cel mai bun exemplu de efect lateral care îmi vine în minte este cel al conotației. Deși analogia e cumva neintuitivă, putem defini un proces de calcul care trece dintr-un cuvânt 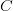într-o definiție 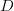a acestuia. Existența conotației denotă formal existența mai multor definiții 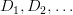care pot fi extrase din cuvântul 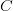, cu toate că 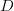este definiția stabilită prin convenție.

Exemplele de mai sus sunt o dovadă a faptului că puritatea joacă un rol foarte important în stabilirea semanticii. Aplicând această concluzie în viața reală, nu putem spune cu certitudine că puritatea este necesară în acest sens. Ea joacă un rol important într-un cadru formal – un text cu valoare juridică trebuie să aibă în teorie o singură interpretare, de exemplu -, însă putem găsi cazuri practice în care este de dorit să avem efecte laterale. Programele pe calculator vor avea întotdeauna efecte laterale – din motive cum ar fi acela că utilizatorul trebuia să poată inspecta rezultatul unei proceduri de calcul -, însă anumite limbaje de programare [iv] tind să încerce (mai mult sau mai puțin) să delimiteze semantic puritatea de cazurile în care pot exista efecte laterale, în special pentru a asigura o oarecare robustețe a programelor.

Plecând de la exemplul conotației, putem spune că aceasta din urmă are un rol artistic important și poate în fapt să îmbogățească expresivitatea actului de comunicare. Fie că este vorba de conotații cu un rol comic sau de exprimări argotice, limbajul natural are de câștigat de pe urma acestui fapt. Pe de altă parte e mai greu de stabilit care este importanța efectelor laterale în actul propriu-zis de comunicare, motiv pentru care nici nu a fost abordat acest exemplu.

Sau poate că dimpotrivă, toate aceste cazuri de utilitate a impurităților sunt artificiale, iar lipsa purității nu face decât să accentueze iadul abstractizării. Cine mai știe.

1. Spre exemplu, fructul galben plin de suc acru având mărimea aproximativă a pumnului unui adult se numește prin convenție lămâie. Notăm că această definiție duce la necesitatea definirii conceptelor care o alcătuiesc, cum ar fi acela de fruct, de galben, acru etc., ajungând astfel la alte concepte de nivel înalt. Pe de altă parte, dacă punem mâna pe o lămâie concretă, putem comunica mai ușor că aceea este o lămâie, lucru practic imposibil în cazul obiectelor abstracte. Mai notăm și că se poate ajunge ușor la sitații neplăcute cum ar fi cea a definițiilor circulare. [↩]
2. Bunăoară limba japoneză are sisteme de scriere și o gramatică care îi afectează puternic expresivitatea. Problema în acest caz nu mai e doar una de translatare în alte limbi, ci de-a dreptul de diferență între logicile de exprimare. [↩]
3. A se observa că folosesc teoria categoriilor drept suport pentru definiții. Fac asta deoarece abstractizările/generalizările conceptelor de funcții și mulțimi, și nu numai, se obțin foarte ușor în cadrul acestei ramuri a matematicii. În acest caz morfismele au prin definiție un singur obiect sursă și un unic obiect destinație. [↩]
4. În special cele bazate pe paradigme funcționale, adică Haskell și dialectele de Lisp. [↩]