să scriem împreună un generator de text markov (iv)
sâmbătă, 26 ian. 2013, 12:40
Am stabilit în cadrul părții a treia a seriei că urmează să construim un generator de text Markov format din două componente:
- O componentă care primește la intrare un model statistic, adică un lanț Markov, și întoarce un text generat aleator. Aceasta a constituit subiectul celei de-a doua părți a tutorial-ului.
- O componentă care primește la intrare unul sau mai multe texte într-o limbă oarecare și construiește pe baza lui, respectiv a lor, lanțul Markov necesar generării de text. În cele ce urmează vom implementa această a doua parte, care este de fapt prima parte a algoritmului în totalitatea sa.
Am observat de asemenea că problema construirii unui model pentru generarea propozițiilor într-o limbă oarecare este teoretic intractabilă. Pe de o parte un „corpus al limbii” complet ar putea fi constituit doar din totalitatea textelor și cuvintelor scrise în limba respectivă. Pe de altă parte limba este o unealtă flexibilă, cu reguli și excepții care pot fi încălcate în diverse contexte, și a cărei formalizare este un subiect de cercetare intens la ora actuală în știința lingvisticii. (mai mult…)
să scriem împreună un generator de text markov (i)
sâmbătă, 15 dec. 2012, 15:29
Invit cititorul de Cărămizi să ia parte la o inițiativă
- (a) destul de rar întâlnită pe blog-urile românești,
- (b) pur didactică,
- (c) destinată programatorilor amatori, profesioniști sau pur și simplu oamenilor cărora le place să-și folosească chestia aia dintre umeri, și nu în ultimul rând
- (d) aparent inutilă.
De fapt punctul (d) e în mare parte fals; stând un pic și cugetând, realizez că ar fi foarte util să urmăriți tutorialul dacă doriți de exemplu să învățați Haskell sau să vă faceți o idee legată de analiză statistică și lanțuri Markov, sau pur și simplu dacă vreți să vă dezvoltați un generator de spam [i]. (mai mult…)
- Nu văd care-i problema. Scopul meu e acela de a le arăta oamenilor cum să folosească cuțitul, nu să le explic cum ar putea să-l vâre în alți indivizi. [↩]
despre statistică: eșantionare.
sâmbătă, 1 dec. 2012, 21:34
Povesteam cu ceva timp în urmă că rolul statisticii este în esență acela de a organiza seturi mari de date în așa fel încât să putem spune ceva despre acestea din urmă. Având un sistem — fizic sau chimic sau informatic sau de orice alt fel, importantă e posibilitatea de a-l analiza cantitativ –, statistica ne ajută deci să îi putem evalua proprietățile dintr-un anumit punct de vedere, nu unicul și nicidecum cel mai eficient din punctul de vedere al consistenței, însă un punct anume de vedere, foarte util prin prisma avantajelor teoretice și practice pe care ni le oferă.
Să presupunem bunăoară că deținem o bucată de metal, a cărei compoziție chimică o cunoaștem apriori. Bucata respectivă este un unic obiect solid despre care știm foarte bine că este în același timp format din o mulțime de atomi legați prin forțe chimice numite și metalice. Despre metale cunoaștem și că au diverse proprietăți fizice cum ar fi conductivitatea electrică sau anumite temperaturi de topire, însă dat fiind numărul mare de molecule dintr-o bucată de metal, ar fi nepractic să cuantificăm aceste proprietăți ale bucății noastre luând în considerare fiecare moleculă în parte. Fizica statistică se dovedește în acest punct a fi esențială pentru a stabili o legătură între efectele mecanicii clasice și/sau cuantice la nivel microscopic și proprietățile macroscopice ale obiectului.
Acesta este un avantaj teoretic al statisticii. Pe de altă parte avantajele practice sunt nenumărate, mai ales dacă alegem drept context Internetul, a cărui cantitate literalmente imensă de date poate fi „minerită” și prelucrată în diverse scopuri, cel mai banal exemplu fiind acela al publicității targetate. În același timp un fișier audio sau o imagine reprezintă ele însele mine de date, acestea putând la rândul lor să fie analizate pentru a extrage cuvinte, respectiv obiecte reale. Putem realiza de exemplu un program care să cunoască un măr într-o imagine oarecare prin alcătuirea unui model statistic și testarea acestuia folosind exemple pozitive și negative [i]. (mai mult…)
- Sigur, o întrebare perfect validă ar fi „cum mai exact facem asta?”. Din fericire Christopher Bishop a scris deja o carte pe temă, cred că am mai menționat-o într-un articol anterior. Ceea ce înseamnă că există deja metode consacrate de a elabora și testa modele statistice, ceea ce face ca lucrurile să fie o idee mai ușoare pentru ingineri. [↩]
despre statistică: distribuții.
sâmbătă, 27 oct. 2012, 18:43
Statistica este domeniul care studiază folosirea unor volume (cât mai mari, sau mai bine zis cât mai generale cu putință) de date spre a extrage ceva util din acestea. Definiția „utilului” diferă de obicei de la o aplicație la alta: în fizică ne poate da o intuiție asupra felului în care se deplasează lichidele sau electronii; în biologie poate explica evoluția anumitor caracteristici ale speciilor; în medicină poate corela evoluția unei boli cu anumiți factori din viața pacientului; în inteligența artificială raționamentul statistic e o metodă de inferență și așa mai departe. Toate acestea au însă un numitor comun.
Am stabilit mai demult că nu e de ajuns să avem date, trebuie să și știm cum să le folosim. Un set de date oarecare e dat de una sau mai multe variabile, cum ar fi de exemplu populația unui oraș măsurată la intervale egale de timp. Variabila din exemplu poate să crească sau să scadă de la momentul 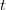
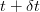
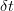
Dacă ați făcut liceul, atunci cu siguranță că vă aduceți aminte că la analiza matematică tendința funcțiilor de a scădea sau de a crește putea fi studiată cu ajutorul derivatelor. Ei, derivata asta, precum și inversa ei, integrala, se dovedește a fi extrem de utilă în algebra probabilităților [i]: putem afirma că există o funcție care exprimă evoluția probabilistică a unei variabile aleatoare, pe care o vom numi densitate de probabilitate. Din aceasta poate fi calculată, printr-o sumă sau o integrală, o distribuție cumulativă, care dă probabilitatea ca variabila aleatoare să se afle într-un interval dat. Și așa am ajuns și la cuvântul cheie „distribuție”. (mai mult…)
- Care pleacă de la spații boreliene și axiome ale lui Kolmogorov și în fine, trece prin teoria mulțimilor și ajunge la chestii care ne depășesc pe noi ăștia care nu suntem experți într-ale matematicilor. Ne limităm la a spune că algebra și analiza matematică sunt foarte utile pentru statistică și probabilități și e bine să aveți o idee despre ele, chit că poate n-o să le aplicați niciodată direct. [↩]
despre statistică: numere mari.
sâmbătă, 22 sept. 2012, 13:19
Dacă matematica e o știință naturală într-un sens anume, atunci putem spune că statistica este acea ramură a matematicii care e cea mai apropiată de concret, adică de natură în sensul ei propriu. E chiar atât de apropiată încât am putea comite eroarea de a rupe statistica de domeniul matematicii și a o introduce bine mersi în alte științe care dispun de dânsa. Legătura e de fapt atât de strânsă încât practicarea științei ar fi imposibilă dacă nu am avea la dispoziție o unealtă atât de utilă cum este statistica. Mai mult, nu am exagera deloc spunând că necesitatea se extinde de la nivelul științei-scientia către cel al științei-knowledge, adică în toate epistemele posibile și imposibile.
Cuvântul „statistică” a fost aparent „coined” [i] de un individ pe nume Gottfried Achenwall, un prusac care a căutat să eficientizeze funcționarea statului prin diverse metode, scriind câteva lucrări notabile [ii] pe temă. Una din lucrări [iii] menționează termenul „statistik” cu referire la afacerile statului și în particular la colectarea și organizarea datelor numerice în cadrul acestuia. De aici și motivul pentru care nu putem vorbi despre date fără a ne gândi la statistică, și vice versa.
Privind problema din alte puncte de vedere, cum ar fi cel al inteligenței artificiale, statistica e un mod de a raționa, la fel ca deducția, care la rândul ei reprezintă o întreagă familie de așa-zise „metode de inferență”. Raționamentul inductiv are atât avantaje cât și dezavantaje față de cel deductiv: de exemplu îmi e foarte ușor să afirm că „toți câinii sunt animale”, pe baza faptului că nu am observat până în prezent vreun câine care să nu fie animal. Pe de altă parte nu pot să trag concluzia că „toate florile sunt galbene” dacă de exemplu eu am observat doar flori galbene pe parcursul existenței mele ca observator, la fel cum nu pot afirma că „Pământul se încălzește” doar pe baza faptului că vara asta a fost mai călduroasă decât cea de acum zece ani. (mai mult…)
- Cuvânt pentru care nu există sinonim în română. [↩]
- Staatsverfassung der Europäischen Reiche im Grundrisse, 1752. [↩]
- Vorbereitung zur Staatswissenschaft, 1748. [↩]